70 résultats trouvés
Revenir à la recherche avancée
Sylviel a écrit:Oui A-B<0 c'est équivalent A<B
donc tu cherches les x tel que
... < ...
Que sais-tu sur la fonction exponentielle ? (Je suis certain que tu as déjà le résultat nécessaire).
Donc on cherche les x tels que e^x < e^a
mais je ne vois pas où ça peut nous amener au tableau de variations...
- par Phoceen
- 09 Mar 2012, 17:25
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
Non, introduire la notation f ne t'apporteras rien. En revanche, parfois, A-B<0 ça peut se résoudre aussi par ...<... (et là c'est trivial grâce à une propriété de l'exponentielle). J'ai cherché un peu partout dans mon cours je n'ai pas trouvé un tel théorème (on a fait qu'un chapitre et il s'appel...
- par Phoceen
- 09 Mar 2012, 17:13
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
Sylviel a écrit:non... tu as e^x - e^a !
exemple : si e^a = 10, alors e^0-10 = -9 < 0
tu cherches les x tel que e^x - e^a <0, comment reformuler l'inéquation ?
Désolé j'ai eu un gros problème mon PC a planté...
donc j'espère que tu pourra reprendre avec moi.
ba f(x) - f(a) < 0 non ?
- par Phoceen
- 09 Mar 2012, 16:55
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
Sylviel a écrit:oui. Maintenant il faut faire le tablaeu de variation de g.
Bon ça devrait aller un peu plus rapidement alors.
Ce n'est pas une fonction de second degré donc aps de calcul de delta on est d'accord ?
- par Phoceen
- 02 Mar 2012, 16:41
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
Sylviel a écrit:oui. Regarde tu as pris : e^a (a-1), tu as bougé un peu x, est-ce que cela à changé quelque chose ?
Ba non...
donc cela donne
= e^x - e^a)
C'est bien cela ?
- par Phoceen
- 02 Mar 2012, 16:32
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
Sylviel a écrit:est-ce que e^a(a-1) dépend de x ? :mur:
Oups. Non, donc pas de forme uv.
là je ne vois pas ce que je dois faire

- par Phoceen
- 02 Mar 2012, 16:06
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
oui. Il faut que tu comprennes que la dérivée c'est "de combien augmente ma fonction quand je bouge un peu x". Exemple : si f'(1)=3 alors f(1+chouilla)=f(1)+3 chouilla. J'ai avancé x d'un chouilla, alors f(x) a avancé de 3 chouilla. De quoi bouge e^a quand x bouge ? De rien ! Normal e^a e...
- par Phoceen
- 02 Mar 2012, 16:00
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
pas vraiment non. Enfin oui mais c'est stupide. Est-ce que 3x c'est de la forme uv ? Oui avec u = 3 et v = x, mais c'est quand même un peu stupide, non ? Oui c'est vrai. Je suis vraiment mauvais en maths... :mur: lé dérivé d'un seul nombre c'est 0, mais la dérivé de 5 x c'est 5 . donc la dérivée de...
- par Phoceen
- 02 Mar 2012, 15:48
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
En fait pour la dérivation le fait qu'il y ait des exponentielles ne change rien. Là tu as un problème de dérivation bien plus basique. la dérivée d'exponentielle c'est exponentielle. Donc (e^x)'=e^x. Par contre e^a c'est un nombre (comme pi si tu veux). Que vaut la dérivée de \pi x ? Donc que vaut...
- par Phoceen
- 02 Mar 2012, 15:32
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
XENSECP a écrit:?? On te dit juste de dériver

=> trivial et d'appliquer en "a"

' = e^x)
, vous êtes d'accord ?
donc
' = e^a)
et
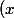' = 1)
donc
' = e^a)
non ?
- par Phoceen
- 02 Mar 2012, 15:30
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
Pléonasme non ? Franchement arriver en terminale et pas savoir dériver bon A Xensecp : je viens à peine de commencer les exponentielles... la dérivation de fonctions habituelles je gère plutôt c'est un des rares trucks que je maîtrise (plutôt) en maths donc ne menlevez pas ça. Après j'avoue qu'ass...
- par Phoceen
- 02 Mar 2012, 14:32
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
Non ce n'est pas trop compliqué. Tu trouveras sur le forum de quoi t'aider à y parvenir. Mais il faut être studieux. Sinon oui, c'est juste. Maintenant essaie de calculer la dérivée de ta fonction en 2. Oui alors par contre je ne suis sûr de rien par contre j'avais tenté tout à l'heure et déjà merc...
- par Phoceen
- 02 Mar 2012, 14:02
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
Je ne veux pas t'affoler mais c'est de jolis lacunes ça quand même... Si f est une fonction dérivable alors la tangeante au point d'absisse a est la droite de pente f'(a) (la dérivée c'est la vitesse de la fonction), qui touche la courbe, donc qui passe par (a,f(a)). Elle a pour équation y = f'(a) ...
- par Phoceen
- 02 Mar 2012, 13:48
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
y=f ' (a) (x-a) + f(a) classique de chez classique Donc je dois réaliser ces opérations ? Allons y alors : Pour f'(a), je dois dériver la fonction entière y = e^x (x-a+1) Pour (x-a), je le garde ainsi je suppose et il faudrait développer après avoir trouvé f'(a)....
- par Phoceen
- 02 Mar 2012, 12:44
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
Bonjour à tous, j'ai un exercice à faire sur les fonctions exponentielles mais je n'y arrive pas malgré les recherches que j'ai fait dès la première question... j'espère réellement que vous pourrez m'aider. Voici l'énoncer : Soit f la fonction définie sur \mathbb{R} par f(x) = e^x On note C ...
- par Phoceen
- 02 Mar 2012, 11:34
-
- Forum: ✎✎ Lycée
- Sujet: Fonctions exponentielle
- Réponses: 35
- Vues: 1525
titine a écrit:Oui !
Et ça tend bien vers 0 quand x tend vers l'infini !
Par contre pour ça, pourriez vous détailler ? Je ne comprend pas pourquoi ça tend vers 0...
Et pour la 2C alors ?
- par Phoceen
- 29 Jan 2012, 19:32
-
- Forum: ✎✎ Lycée
- Sujet: Limites et continuité (bien entamé)
- Réponses: 15
- Vues: 611
Donc il y a une asymptote verticale x = 1 ? Je ne voit pas ça sur ma calculatrice... mais bon. Donc du coup je dois faire quoi pour le 2.B ?
Dois-je calculer f(x) - y ?
- par Phoceen
- 29 Jan 2012, 18:35
-
- Forum: ✎✎ Lycée
- Sujet: Limites et continuité (bien entamé)
- Réponses: 15
- Vues: 611
