Forum de Mathématiques: Maths-Forum

Je me disais qu'il me manquait un cas, mais je n'ai pas voulu m'acharner, gros défaut...
Merci beaucoup encore une fois ! :)

Bonjour à tous, Après m'être bien cassé le nez pendant une bonne heure, je viens quérir de l'aide auprès de vous, voire la réponse si vous avez un peu de temps, car là je ne vois pas la réponse à ma question... On suppose que X suit la loi uniforme sur [-1 ; 2]. 1. Montrer que Y=X^2 est un variable ...

Bref dans tous les cas j'ai su me débrouiller en m'appuyant sur vos réponses. J'ai ouvert une discussion où dans un premier cas, j'excluait le 1 et j'utilisais le critère de comparaison, et dans le second cas où x=1 j'ai utilisé le critère des séries alternés après avoir jeté un coup d’œil sur inter...

Critère des séries alternées, jamais ? Au pire si tu veux de la comparaison, tu dis que \frac{x^n}n \leq x^n et tu te retrouves à regarder une série géométrique. J'espère que ça au moins tu connais. Oui tout de même je connais cette dernière. Je pense que je vais partir sur ça. Il faut dire que le ...

J'ai vu les trois critères, celui d'absolue convergence, de comparaison et de négligeabilité. Je pensais utiliser celui de négligeabilité après avoir appliqué la valeur absolue, mais de même le cas où x=1 me posera problème...

Donc j'ai essayé de l'appliqué... Si je comprends bien la situation, il faut que j'applique la valeur absolue pour avoir l'expression \frac{x^n}{n} . Avec cela j'applique le critère d'Alembert qui me permet de trouver que \lim_{n\to +\infty}(\frac{x}{1+\frac{1}{n}})=x Enfin je ne sais pas co...

deltab a écrit:Bonsoir


Vraiment. Refais l'étude de convergence absolue en utilisant le critère de D'Alembert par exemple. Il te restera un cas à étudier.

Je ne connaissais pas du tout ce critère. Je vais voir et essayer.

J'applique la valeur absolue à l'expression, puis je trouve . Certes mais ce n'est pas quelque chose de connu, et je ne vois pas quel critère utilisé par la suite...

Bonsoir ! Afin de reprendre les (bonnes) habitudes de la rentrée et me remettre dedans, il me faut un peu de temps pour retrouver toutes les méthodes, et surtout celles qui conviennent. Pour le moment je dois montrer la convergence d'une série de terme général \frac{(-1)^{n+1} \times x^n}{n}...

J'avais entrepris cela au début, mais autant pour moi j'avais fais une simple erreur de signe... Mortelle lorsqu'il s'agit de chercher le signe. Merci infiniment !

C'est quoi ta fonction de départ ? (épargne-nous un calcul de primitive odieux s'il te plaît) Normalement il ne devrait pas y avoir de calcul de primitive... Ma fonction de départ était : Définie sur R^+ par : f(x)= \frac{ln(1+x)}{x} si x>0 sinon 1 si x=0 . La première dérivée est :...

Bonsoir à tous. Voilà, je viens de calculer la dérivée seconde d'une fonction, et on me demande de montrer que la fonction est convexe. En toute logique, je me dois de montrer que la dérivée seconde est positive sur l'intervalle considéré. Le hic, c'est que je ne sais pas comment m'y prendre après p...

D'accord c'est bien plus clair maintenant !
Merci beaucoup en tout cas, j'ai tendance à beaucoup trop me prendre la tête avec les questions de rédaction...

En faisant un développement limité d'ordre 2 en 0, selon la méthode utilisée par notre professeur, je tombe sur un problème de négligeabilité. Voici la démonstration : \frac{1}{x}\times\frac{1}{x+1}-\frac{1}{x^2}\times ln(x+1) = \frac{1}{x}(1-x+x^2+x^2\epsilon_1 (x))-\frac{1}...

Le décomposition en éléments simple ne mène à rien, et le développement limité n'est pas concluant... Après il se peut que je fasse des erreurs, le temps de se remettre dedans !

Bonjour !
Je suis certain que cette limite n'est pas sorcier, mais ça fait une heure que j'y suis et j'ai essayé toutes les méthodes que je connaissais. La voici :

Merci beaucoup !

Bonsoir à tous ! Je viens quérir une précieuse aide après avoir réfléchi toute une journée sur un (super) exercice dont je vous en fais part : On considère l'application f définie sur \mathbb{R} par : f : \mathbb{R} \rightarrow \mathbb{R} x \neq 0 \mapsto f(x)=2+\frac{x}{1-e^x 0 \mapsto f...

Non pardon j'ai confondu. Car dans la suite de mon exercice on me demande lorsque U_o \in ]e-1 ; +\infty[ , dans ce cas (U_n)_{n \in \mathbb{N}} est croissante. Mais concernant l'intervalle ]0;e-1[ j'ai réussi à correctement conclure. Décidément, ça ne m'arrange pas d'écrire des maths sur or...

Oui c'est exactement ce que j'ai fais et j'ai pu terminer l'exercice !
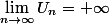, donc si alors la suite est croissante.
En tout cas merci beaucoup pour ton aide !

Si , donc donc 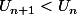, donc la suite est décroissante et par conséquent car
Super j'ai compris, merci infiniment de ton aide ! :we: