Forum de Mathématiques: Maths-Forum

girdav a écrit:En dérivant des deux côtés de l'équation.

Petite question pouvez vous m'expliqer comment deriver une integrale car a chaque fois j 'enleve juste l'integrale mais selon les bornes c'est faux

girdav a écrit:Pour la deux, est dérivable; on peut chercher une équation différentielle satisfaite par .

Euh je ne vois pas comment poser une equa diff ?

Il faut y aller à coup de \varepsilon : pour \varepsilon>0 fixé, on peut trouver \delta>0 tel que si |x-1|\leq \delta , alors |f(x)-f(1)|\leq \varepsilon . Puis regarde l'intégrale sur (0,1-\delta) et (1-\delta,1) . D'accord, merci beaucoup 2) J'ai essayé de chercher...

girdav a écrit:Si, tu sais qu'elle est continue, c'est suffisant ici.

je n'arrive pas à montrer la limite car n tend vers + infini ce qui me bloque pour trouver 0, car même si l'integrale tend vers 0 j 'ai une forme indeterminée

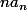
girdav a écrit:Pose et montre que tend vers .

Comment puis je montrer vu que je ne connais rien sur f ?

Bonjour, pouvez vous m'expliquer comment resoudre ces questions. 1) Montrer que integrale de t=0 à 1 de t^n f(t) = f(1)/n + o(1/n) on suppose que f est continue sur [ 0,1 ] 2) Déterminer les f continues tel que pour tout x dans R, f(x) + int de 0 à x de (x-t) f(t) dt = 1 3) Soit Ix = int de 0 à pi/2...

Mais c'est exactement ce que tu voulais montré mais on l'a fais dans le désordre. Il faut que tu reparte de : ln( 1+ exp(2x) / 1 +exp(-2x) ) = ln( exp(2x) * ( exp(-2x) + 1 / 1 +exp(-2x) ) ) = ln( exp(2x) ) = 2x :zen: Euh non, il y a quelque chose qui me bloque en montrant que : exp(2x) * ( exp(-2x)...

antonyme a écrit:Il ne faut pas multiplier le dénominateur :langue:

Ah oui je suis allez trop vite

Du coup j'ai du

(exp(-2x) + 1) / (1 + exp(-2x)) = 1

C'est un peu bizarre ca me donne 1 = 1 du coup y a pas d'interet ?

antonyme a écrit:Si tu suis le conseil de gdlrdc tu obtient :
To be continued...

justement mon probleme est que je tombe sur :

( exp(-2x) + 1 / exp(-2x) + exp(-4x) ) = 1

et la je ne sais pas quoi faire

antonyme a écrit:En faite là il y a surtout une parenthèse ouverte en trop. Mais ln porte bien sur la fraction globale.

le ln porte sur la fraction mais je suis quand même bloquer

gdlrdc a écrit:Tu aimerais montrer que ( 1+ exp(2x) / 1 +exp(-2x) ) = exp(2x).
ce qui reviens à montrer quoi en multipliant chaque membre de l'égalité par exp(-2x) ?

En multipliant par exp(-2x), on obtient :

ln ( exp(-2x) + 1 / exp(-2x) + exp(-4x) ) et la je ne sais pas quoi faire non plus

Bonjour,


J'ai juste besoin de votre aide pour montrer que

ln( ( 1+ exp(2x) / 1 +exp(-2x) ) = 2x

Je bloque dessus j'ai essayé de résoudre ( 1+ exp(2x) / 1 +exp(-2x) ) en multipliant en haut et en bas par le denominateur mais je n'aboutit à rien.

Merci

ev85 a écrit:Et pendant que tu y es, ?

Conclusion : ?

En conclusion cela vaut une constante

Mais du coup je ne vois pas le lien avec int de 0 à +inf de exp(-t²) ?

ev85 a écrit:Donc tu ne t'es pas relu.

Calcule f(0) et g(0).

Donc ? Non je me suis relu mais je ne vois pas mes erreurs, on montre que f² + g est une constante pour tout x donc je fais pour tout x .

f0) = 0

g(0)=arctan(1) - arctan(0) = arctan(1)

ev85 a écrit:Bon tu écris à peu près n'importe quoi. Relis-toi.
La constante, tu peux la calculer pour x=0, non ?

Tu coup je ne comprend pas ce que vous voulez dire, pouvez vous developper un peu plus ?

Merci par avance

2/ \dfrac d{dx}(f^2(x)+g(x)) = 2f(x)f'(x) + g'(x) Or 2f(x)f'(x) = 2e^{-x^2} \int_0^x e^{-t^2} \,dt et g'(x) = 2x \int_0^x e^{-x^2(1+t^2)} \,dt . Un changement de variable u = xt dans cette intégrale term...

Bonjour, merci de m'aider : Soient f, g définies par : f(x) = int e 0 à x de exp(-t²) dt g(x) = int de 0 à 1 de [ exp(-x²(1+t²)) ] / ( 1 + t²) dt 1) Montrer que f et g sont de classe C1 sur R. 2) Dériver l'expression f(x)² + g(x) 3) Montrer que f² + g est une constante 4) En déduire la valeur de int...

ev85 a écrit:Néant toi-même !

Mon c'est pas n'importe qui, c'est un qui va bien. Par exemple la partie entière de .

Mais pourquoi on a le droit de majorer par la partie entiere de A-1/2 pourquoi forecement c'est ca

Tu regardes \int_0^A \dfrac{\sin x}x\,dx tu l'écris \int_0^{2n+1} \dfrac{\sin x}x\,dx+\int_{2n+1}^A \dfrac{\sin x}x\,dx avec un n qui va bien et tu majores sauvagement la dernière intégrale (en valeur absolue bien sûr, il y a des limites à la sauvagerie) Du coup, on peut sauvagement majorer par int...

Ah oui on se sert de la question du dessus.

Par contre pour la derniere je dirai oui mais je ne sais pas comment le prouver

Merci