Forum de Mathématiques: Maths-Forum

Bonjour à vous deux.

Merci GaBuZoMeu en effet.
Merci tournesol !

Ma question est certainement toute bête. Pour conclure lors d'une démonstration, l'auteur affirme qu'étant donné p^{a}\leq p^{n} , on a a\leq n . p désigne un nombre premier, a et n sont des entiers naturels. Je voulais savoir quel théorème a été utilisé pour affirmer ça. La réciproque c'est normal ...

J'enchaîne les bourdes. J'écris tout :
Dans N - {1} muni de la divisibilité, 2 est un élément minimal, tous les nombres premiers d'ailleurs.
Dans N - {0}, il n'y a pas de maximum.

Voilà, j'espère que cette fois-ci on est bon

Lapsus c'est pour les entiers non nuls que je me référé.
Et pour ta question : 0 évidemment.

Oui, je vois bien la chose, avec un diagramme de Hasse.
Si j'ai bien compris, avec E = {0,1} et P(E)* = {{1}, {2}, E} le singleton {1} est un élément minimal pour l'inclusion. Mais du coup y a aussi {2} donc pas unicité.

Merci lyceen95.
Un élément maximal, en gros c'est un maximum local ?

Ah ! Mais du coup, vos deux réponses se contredisent un peu non ? @lyceen95 affirme que la contraposée n'a pas de sens pour la divisibilité et @tournesol affirme que "a different de x implique que a n'est pas inférieur ou égal a x , ie a superieur à x ou a n'est pas comparable avec x ". Je...

Bonjour, Je donne une définition de la notion d'élément maximal : Soit (E,\preceq ) un ensemble ordonné et a un élément de E. On dit que a un élément maximal de E si : \forall x\in E,a\preceq x\Rightarrow a=x Par contraposée cela donne donc : \forall x\in E,a\neq x\Rightarrow x\prec a Je vou...

D'accord @tournesol et merci de ta patience ! Je rédige maintenant tout ça à ma façon.

Du coup je reprends le raisonnement de @tournesol.
x dans I mais pas dans J et y est dans J mais pas dans I.
I et J sont non disjoints : il existe un élément a dans I n J.
Maintenant, il s'agit de montrer que x <= a <= y.

D'accord. Dans ce cas, il faut une disjonction de cas plus stricte. 1) x et y sont dans I, dans ce cas [x,y] inclus dans I qui lui-même inclus dans I u J. 2) x et y sont dans J, dans ce cas [x,y] inclus dans J qui lui-même inclus dans I u J. 3) x et y dans I n J (possible car I et J sont non disjoin...

Il y a un truc qui ne va pas, il est possible que a <= x après tout puisque x peut être aussi dans J. Tu as exclu le cas où y est dans I mais reste dans J.

Sur un dessin, il est clair que x<=a<=y, mais je ne vois pas comment le justifier.
J'ai pensé à la borne supérieure mais ça n'aboutit pas.

Peux-tu me dire qui est "a" dans ce que tu as écris ?

Merci, j'essaie de rédiger ça !

Bonjour, Je commence par donner une définition : Soit I un sous-ensemble de R. I est un intervalle de R si : \forall (x,y)\in I^2,x\leqslant y\Rightarrow [x,y]\subset I Je dois montrer que l'intersection de deux intervalles de R est un intervalle de R. J'ai bien réussi. Je dois aussi montrer...

Merci !

La récurrence en gros c'est : "pour toute partie A de N et pour tout entier p, si p est le plus grand élément de N, alors A est fini".

L'HR suppose que pour toute partie de plus grand élément inférieur ou égal à p ...
Tu es sûr que c'est une récurrence classique ?

Bonjour, Ma question est au niveau de cette démonstration : https://zupimages.net/up/21/46/wej1.png En b), l'auteur utilise l'hypothèse de récurrence en p mais pour les entiers naturels inférieurs ou égaux à p. C'est donc une récurrence forte même s'il ne l'a pas dit explicitement ?

Je voulais écrire 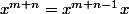quand on suppose m+n > 0



Oui mais - |m| < 0 alors que n > 0 , on ne peut donc pas utiliser la formule puisque c'est ce qu'on veut démontrer.