5 résultats trouvés
Revenir à la recherche avancée
Dans mon problème les valeurs propres de  représentent les masses de deux particules. Elles sont donc positives. De plus je peux encore faire l'hypothèse que que
représentent les masses de deux particules. Elles sont donc positives. De plus je peux encore faire l'hypothèse que que  et
et  ont un déterminant égale à un.Dans ce cas la je crois que la relation est valide et que
ont un déterminant égale à un.Dans ce cas la je crois que la relation est valide et que 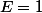
- 18 Nov 2010, 22:05
- Forum: ✯✎ Supérieur
- Sujet: Relation a montrer
- Réponses: 8
- Vues: 560
Un seul mot merci! C'est la première fois que je viens sur ce forum. Je n'hésiterai pas à la refaire. En effet Il faut ajouter l'hypothèse qu'on choisi U et V tel que d_1 = d_2 avec valeurs propres non nulles. Ensuite je pense avoir compris ta preuve. De plus j'ai besoin de cette relation pour une m...
- 18 Nov 2010, 13:22
- Forum: ✯✎ Supérieur
- Sujet: Relation a montrer
- Réponses: 8
- Vues: 560
Effectivemen U et V sont unitaires j'ai corrigé l'énoncé. Désolé ce n'était pas très propre de ma part...
- 17 Nov 2010, 17:56
- Forum: ✯✎ Supérieur
- Sujet: Relation a montrer
- Réponses: 8
- Vues: 560
- 17 Nov 2010, 17:49
- Forum: ✯✎ Supérieur
- Sujet: Relation a montrer
- Réponses: 8
- Vues: 560
Relation a montrer
Bonjour, Je suis bloqué sur une relation. Je ne sais pas si elle est valide ou non. Soit une matrice A et deux matrices unitaires U et V J'aimerai montrer les implication suivantes: Si UA^\dagger A U^\dagger = d_1 et V A A^\dagger V^\dagger = d_2 avec d_1 et d_2 diagonales Alors V A U^\dagger = D av...
- 17 Nov 2010, 16:35
- Forum: ✯✎ Supérieur
- Sujet: Relation a montrer
- Réponses: 8
- Vues: 560
- 5 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
