Forum de Mathématiques: Maths-Forum

Est-ce que vous pouvez m'expliquer brièvement comment vous en arrivez là alors car c'est justement ça qui me pose problème?

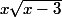
Et est-ce que dériver revient bien à la même chose ?

Merci.

Simplifier \sqrt{x^2(x-3)} en \sqrt{x^2}\sqrt{x-3} ? Je vais essayer... Ce qui m'embête c'est lorsque je dérive, vaut-il mieux factoriser ou pas ? Car lorsque je fais ma dérivée seconde, je me retrouve avec un numérateur très long et assez lourd à digérer pour la suite... Edit : J'ai trouvé ...

En m'intéressant uniquement à ?

d'où dom f : 3 à + l'infini

Merci pour l'astuce Latex !

Bonjour, Je suis bloqué sur la dérivée seconde d'une fonction qui est : y= \sqrt{x^2(x-3)} Ma dérivée première est : 3x.(x-2) / 2 \sqrt{x^2(x-3)} Par contre pour la dérivée seconde, je me retrouve avec une équation sacrément longue et lorsque j'essaie de la simplifier, je ne tombe ja...