Forum de Mathématiques: Maths-Forum

diox a écrit:je sui en terminale ES

dac jessaye mé ne menveu pa si je fait des fautes très bete lol
alors : g(x)=2-x et u(x)=x²
donc g'(x) =-1 et u'(x)= 2x
=> dapres la formule 2x*(-1) =-2x donc la fonction est décroissante c kelke chose kom sa ? ^^

Rebelle_ a écrit:Hum ici on notera plutôt f'(x) = u'(x)*g'(u(x)).
Au fait, es-tu en Première ou en Terminale ?

je sui en terminale ES

Rebelle_ a écrit:C'est flou mais je pense que tu veux dire qu'il veut que vous calculiez la dérivée pour en étudier le signe et en déduire les variations de f ?
C'est possible ! Quelle est la formule de la dérivée d'une fonction composée ?

f(u)' x (x) = f'[u(x)] x u'(x) c sa ? =p

Rebelle_ a écrit:Attention, le signe d'une fonction est bien différent de son sens de variation

enfaite j'ai un nouveau prof et il ma dit de faire f ' (x) x u' je c pa pk ?

Hum il faut apprendre ton cours :P Soit une fonction f définie sur I telle qu'étant la composée de deux fonctions u et v, si ces deux dernières ont le même sens de variation (resp. sont de sens de variation contraires) alors leur composée est croissante (resp. décroissante) sur I. Saurais-tu le dém...

Eh bien voilà, on a terminé pour le premier ! Nota bene, quand on parle de fonctions composées il est bon de faire attention aux intervalles considérés pour prévenir tout problème d'existence. Tu peux essayer le second ? ;) oui oui jvé faire le second tout de suite mai jaimerai savoir comment je do...

Oui c'est à peu près ça, tu as l'idée, sauf qu'on écrira plutôt (g(x))² = f(x) ou g² = f ;) Alors, pour obtenir f on utilise deux fonctions : la fonction g définie sur R telle que g(x) = 2-x et la fonction u définie sur R par u(X) = X². En fait, ici on pose X = g(x). Ainsi, on a f = u o g (lire &qu...

B'soir :) On regarde la première ensemble ? On a la fonction f (définie sur R) par f(x) = (2-x)². Ici, on prend une fonction g(x) = 2-x définie sur R de même. Peux-tu trouver la relation entre g et f ? :) ^^ slt dsl si je di nimporte quoi je ne comprend pa trop les fonction composé :: alors je diré...

le theme est sur la dérivation de fonction composé alors tout d'abord je ne comprend pa comment écrire f sous la forme de fi (u) et je doit en suite etudier son sens de variation f(x)=(2-x)² f definie sur [3/5 ; +inf] f(x)=racine (5x-3) f definie sur ]-inf;1] f(x)=racine (1-x) f define R -(2) f(x)=1...

diox a écrit:donc si je comprend bien en -infini assyptote horizzontale ;; en 2 et 7 assymptote verticale ;; en +infini assyptote horizontale

ma réponses est elle juste ?

je doit comparer deux droites d'ajustement de 1975 a 1999 et DE 2000 a 2003
pour la premiere periode je trouve y= 131,6x-255444,7 et pour la deuxieme periode je trouve y= 26,6x-45040,9 comment je doit faire pour comparer ces deux droites d'ajustement ?

Jimm15 a écrit:Regarde le quatrième message de CE SUJET.

donc si je comprend bien en -infini assyptote horizzontale ;; en 2 et 7 assymptote verticale ;; en +infini assyptote horizontale

Je t’écris les réponses car je ne comprends pas ce que tu écris donc je ne sais pas si c’est juste ou faux. En tout cas, j’espère que tu ne rédiges pas comme ça sur ta feuille car ce n’est pas correct. Déterminons la limite de j en – \infty \lim_{x \to -\infty}f(x)=1 et \lim_{x \to 1}\frac{...

diox a écrit:daccord ^^ pour le j j' ai fait lim j(1/1) =1 vers -inf
lim j(1/0) = indefini vers 2 ; lim j(1/0) = indefini vers 7 ; lim j(1/+infini )= 0

est ce que ce que j'ai trouvé et correcte ?

En +\infty , il n’y a aucune asymptote à la courbe de h puisque \lim_{x \to +\infty}h(x)=+\infty . Cela signifie que h(x) peut être rendu « aussi grand que l’on veut » dès que x est assez grand. En – \infty , la droite d’équation y=1 est asymptote horizontale à la courbe de h , d’ap...

Jimm15 a écrit:Lorsque , on dit que la droite d’équation 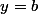est asymptote horizontale à la courbe de en –.

donc je doit mettre assymptote horizontale d'equation y= +infini car lim (+infini )= +infini et lim (1)=1

Jimm15 a écrit:Non. C’est une asymptote horizontale. J’aimerais que tu me précises l’équation de la droite qui est asymptote à la courbe de et si c’est en – ou bien en ?

dsl je vois pa =P

C’est juste mais la rédaction est strictement inacceptable. On écrit : \lim_{x \to -\infty}f(x)=1 et \lim_{x \to 1}\sqrt{x}=1 D’où \lim_{x \to -\infty}h(x)=1 \lim_{x \to +\infty}f(x)=+\infty et \lim_{x \to +\infty}\sqrt{x}=+\infty D’où \lim_{x \to +\infty}h(x)=+\inft...

Non, il n’y a aucune asymptote en 2 ou en 7 pour h pour la simple et bonne raison que : h(2)=\sqrt{f(2)}=\sqrt{0}=0 et h(7)=\sqrt{f(7)}=\sqrt{0}=0 As-tu étudié les limites de h en - \infty et en + \infty ? Qu’en déduis-tu ? g fait lim h (1) vers -inf = 1 etlim h (+in...

Jimm15 a écrit:Par définition, une limite est quelque chose qui n’est jamais atteint. On s’en rapproche sans jamais l’atteindre. Or, ici, on atteint bien les deux nombres !!

donc il y a deux assymptote en 2 et en 7 c'est ca ? pour le j comment je fait pour étudié sa limite ? en + linfini par exemple