77 résultats trouvés
Revenir à la recherche avancée
chan79 a écrit:rapidement
(1+x+1-7x-2-5x+0(x))/x qui tend vers -11
à vérifier
rien compris, la réponse comme ça sa ne m'aide pas vraiment
- par Mr.DDR
- 03 Juin 2012, 22:37
-
- Forum: ✎✎ Lycée
- Sujet: limite et développement limité
- Réponses: 4
- Vues: 1191
pour calculer cette limite il faut utiliser le développement limité mais je ne sais plus comment faire, help pls
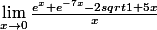
- par Mr.DDR
- 03 Juin 2012, 10:39
-
- Forum: ✎✎ Lycée
- Sujet: limite et développement limité
- Réponses: 4
- Vues: 1191
HA oui !!!
ça donne :
ln(e^x(2+1/(e^x) - ln(2+1/e^x) = x
x = ln(e^x)
ln(e^x(2+1/(e^x) = ln(e^x) + ln(2+1/e^x)
ln(e^x(2+1/(e^x) = ln(e^x(2+1/e^x))
merci :)
- par Mr.DDR
- 02 Juin 2012, 20:01
-
- Forum: ✎✎ Lycée
- Sujet: exponentielle terminale s
- Réponses: 5
- Vues: 455
ln(2e^x(1+1/(2e^x) = x + ln(2+2/2e^x)
ln(2e^x(1+1/(2e^x) = x + ln(2+1/e^x)
ou on factorise par e^x, ce qui donne:
ln(e^x(2+1/(e^x) = x + ln(2+1/e^x)
et ensuite ?
- par Mr.DDR
- 02 Juin 2012, 19:53
-
- Forum: ✎✎ Lycée
- Sujet: exponentielle terminale s
- Réponses: 5
- Vues: 455
Bonjour je ne sais pas comment résoudre cette équation merci de maider :
f(x)= ln(2e^x +1)
montré que f(x)= x+ln2+ln(1+(e^-x)/2)
Comment procéder ?
ln(2e^x +1) = x+ln2+ln(1+(e^-x)/2)
- par Mr.DDR
- 02 Juin 2012, 18:44
-
- Forum: ✎✎ Lycée
- Sujet: exponentielle terminale s
- Réponses: 5
- Vues: 455
ok

donc pour pas me tromper ensuite le quel est bon
E(x) : y(x) + 2y(x) = 0
y(x) =

ou
y(x) =

(dsl j'arrive pas à faire la racine)
- par Mr.DDR
- 18 Fév 2012, 13:05
-
- Forum: ✎✎ Lycée
- Sujet: équations différentielles
- Réponses: 8
- Vues: 570
Bonjour peut-ont maider : Vérifié pour a) et b) y(0) = 2 et y(0) = -1 a) y = cos7x y = 1/7sin7x +k(1) ; k(1) = -1 y = -1/49cos7x + k(1)x + k(2) ; k(2) = 2+1/49 b) y = 1/((x-1)^6) y = -1/(5(x-1)^5) + k(3) ; k(3) = -6/5 y = 1/(5/4(x-1)^4) + k(3)x + k(4) ; k(4) = 2-4/5 1- E(x) : y(x) + 2y(x) ...
- par Mr.DDR
- 17 Fév 2012, 16:25
-
- Forum: ✎✎ Lycée
- Sujet: équations différentielles
- Réponses: 8
- Vues: 570
je n'avait pas les formules pour tan bref ^^
oui sans oublier +k à chaque fois :)
- par Mr.DDR
- 17 Fév 2012, 12:39
-
- Forum: ✎✎ Lycée
- Sujet: primitive tS
- Réponses: 13
- Vues: 674
J(x) = -1/3(cos(x^3))
là normalement c'est bon en dérivant j'ai bien j(x)
N(x) = 2/3(2+sinx)^(3/2) le ^(1/2) faut bien que je m'en souvienne
i(x) c'était un petit bonus dans les exos j'ai pas les formule ...
merci pour le reste
- par Mr.DDR
- 16 Fév 2012, 20:14
-
- Forum: ✎✎ Lycée
- Sujet: primitive tS
- Réponses: 13
- Vues: 674
j = sin(u)*u'
J = 1/2-cos(u)^2
u' = 1/3*3x^2
J = -1/3(cos(x^3))^2
- par Mr.DDR
- 16 Fév 2012, 15:58
-
- Forum: ✎✎ Lycée
- Sujet: primitive tS
- Réponses: 13
- Vues: 674
st00pid_n00b a écrit:h(x): Encore une erreur de signe
ah oui en effet H(x) = cos(\pi/6-x)
i, oui c'est le bon énoncé
pour j c'est le cube de x
ok je vais voir tout ça
- par Mr.DDR
- 16 Fév 2012, 15:32
-
- Forum: ✎✎ Lycée
- Sujet: primitive tS
- Réponses: 13
- Vues: 674
je vois où est mon erreur dans H
je ne suis pas sur :
H(x) = -cos(\pi/6-x)
moi aussi ça me parait dur ^^, c'est le seul avec un tan que l'on est eu
- par Mr.DDR
- 16 Fév 2012, 15:01
-
- Forum: ✎✎ Lycée
- Sujet: primitive tS
- Réponses: 13
- Vues: 674
Bonjour, j'aurai besoin d'aide f(x) = -2x^3 +3x F(x) = (-x^4)/2 +(3x^2)/2 g(x) = 6/(x^3) G(x) = -3/x^2 h(x) = sin(\pi/6-x) H(x) = -\pi/6*cos-x i(x) = 2-tan^{2}x I(x) = ??? j(x) = x^2*sinx^3 j(x) = u^n*u^ ??? k(x) = \frac{7x}{sqrt{1+x^2}} k(x) = \frac{u^}{sqrt{u}} u...
- par Mr.DDR
- 16 Fév 2012, 14:38
-
- Forum: ✎✎ Lycée
- Sujet: primitive tS
- Réponses: 13
- Vues: 674
donc la primitive c'est ça puisque c'est égale à la dérivé
' = sqrt{x})
non ?
- par Mr.DDR
- 24 Nov 2010, 18:58
-
- Forum: ✎✎ Lycée
- Sujet: primitive/dérivée
- Réponses: 11
- Vues: 403