Forum de Mathématiques: Maths-Forum

Super ! Merci beaucoup !! :ptdr: :we: :lol3: !!

oui ! j'ai fait le tableau de variations de et je trouve qu'elle n'est jamais négative, mais qu'elle est définie sur R.
c'est juste ? Et c'est démontré ou il manque quelque chose ?

Bonjour, j'ai un problème dans un exercice.
Je dois justifier que la fonction est définie sur
Mais voilà je n'y arrive pas vu que on a vu qu'un logarithme néperien n'est pas définie pour tout x ...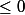
Pouvez vous m'aider ?

Oui bien sur !! Et merci beaucoup pour votre aide !! bonnes fêtes

ok : Supposons que \Phi est solution de (E) et montrons f est une primitive de de k : on part de \phi ' (x) - 4 \Phi (x) = - \frac{4e}{(1+e^{-4x})^2} et on arrive à f'(x) = e\times h(x) Réciproquement, on suppose que f est une primitive de k et on mont...

J'ai réussi le 1er cas : Dans le premier cas tu dis que \Phi est solution de (E) (tu as donc une relation entre \Phi et \Phi ')... En simplifiant tu arrives normalement à l'expression f'(x) = e\times h(x) merci beaucoup =) par contre le deuxième cas je comprend pas du tout... Je ...

oulà je suis vraiment désolée effectivement j'en suis à la 2a...

oups ! ah oui vous me l'aviez dit en plus... Du coup ça donne f(x) = - \frac{e}{1+e^{-4x}} +C Maintenant que j'ai montré que si f est primitive de k, \Phi est solution de (E), et je dois montrer que si \Phi est solution de (E), f est primitive de k, c'est ça ? le problème c'est qu'en partant...

H(x)= - +C (C )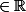

Donc f(x) = e H(x)
f(x) = -

Mais on est censé commencer de l'équation différentielle (E) puis arriver à l'expression de f(x), non ?

Non, bien sur que non, j'ai mis l'exercice en entier pour que vous ayez tout sous les yeux.
Et puis il n'y a pas que ces deux exos, les autres je les ai réussi, c'est seulement ces questions ça fait longtemps que je cherche , mais je n'y arrive vraiment pas...

Bonjour j'ai un exercice de mon DM où je suis bloquée... Voilà l'exercice : Soit h la fonction définie sur R par h(x)= \frac{-4e^{-4x}}{(1+e^{-4x})^2} Soit (E) l'équation différentielle y'-4y = \frac{-4e}{(1+e^{-4x})^2} 1/ Déterminer l'ensemble des primitives H de h. 2/ S...

Bonjour, désolée pour le temps de réponse...

En fait j'ai fait une erreur dans l'énoncé :doh:
A la question 2)b., ce n'est pas mais ...
C'est pour ça que je n'y arrive pas...

Bonjour à tous. J'ai un problème avec mon DM dont voici l'énoncé : L'objet de cet exercice est d'étudier la fonction g définie sur [ 0 ; +\infty[ par: g(t) = \frac{1-e^{-t}}{t} si t>0 et g(0)=1 1-a) établir que g est continue en 0. b) Déterminer la limite de g en + \infty 2°) a) Pour tout t>0, calcu...

cool =) Pour le début de la question 2) je suis désolée mais je n'ai vraiment pas compris à partir de : n^4 =< (n+1)^3[(n+1)-1] et donc à n^4 =< n(n+1)^3 ce qui est évidement vrai. Parce que je ne voit pas comment on passe de (n+1)^4 à [(n+1)-1] ... :mur: et pour la fin du 2, j'ai eu beau finir mon ...

Pour la fin du 2) j'ai trouvé pour x= \frac{1}{n^2} \frac{1}{n^2}-\frac{1}{6n^6} \leq sin{\frac{1}{n^2}} pour x= \frac{2}{n^2} \frac{2}{n^2}-\frac{8}{6n^6} \leq sin{\frac{2}{n^2}} et pour x= \frac{n}{n^2} \frac{n}{n^2}-\frac{n^3}{6n^6} \leq sin{\frac{n}{n^2}} C'est juste ? (je suis en train de cherc...

ah j'avais pas vu votre message de 15h46... désolée =)

ça y est je crois avoir trouvé ! (enfin)



donc
et
C'est juste ?

... En fait je ne vois pas d'où vient le 3/4 ...

ah ! et je trouve
C'est bon ? :hein:

ok merci =)

J'ai réussi les questions jusqu'à la 4.
Comment peut-on connaître le signe de f'' à part avec la calculette ?