Forum de Mathématiques: Maths-Forum

Excuse moi mais sauriez vous comment joindre les 2 limites dans cette exemple??

Non il suffit que la limite soit finie pour avoir une asymptote oblique. Si elle valait 0 l'asymptote srait un peu spécial (quoi d'ailleurs)... Asymptote horizontale ??? Je n'arrive pas à faire le passage entre les 2 limites!! :( 3heures sur la même question, sa commence à me gonfler :triste:

On a f(x) = \frac{g(x) - g(0)}{x-0} où g(x) = sin(x). \lim_{x \to 0} \frac{g(x) - g(0)}{x-0} = g'(0), or ici g'(x) = cos(x) et donc g'(0) = 1 et de fait : \lim_{x \to 0} \frac{sin(x)}{x} =1 Donc \lim_{x \to + oo} f(x) -\frac{x}{2} = 1 Ce qui est bizarr...

Arnaud-29-31 a écrit:Ahh donc ca fait quoi ??

Maintenant la même avec ... ^^

Je suis même pas sur de mon résultat donc Je verrais ce calcul plus tard ou jamais......

Quelqu'un peut me dire si la limite = 1 où si je me suis planté

Rebelle_ a écrit:Tu es en train de balancer deux des questions de mon dernier DS...
Si tu veux M. le posteur (je suis une fille sage =P) je peux te donner les autres pour t'entraîner

C'est bien gentil mais entre moi et les maths, c'est pas une belle histoire. Moins j'en fais, mieux je me porte :lol3:

Je trouve que ma limite = 1 c'est normal ??(Je parle de ma limite que je cherche, celle de f(x)-x/2)

Rebelle_ a écrit:Tu es sûr de ce que tu nous dis là ?

Nan je finissait mon calcul d'avant que j'ai foiré donc c'est faux

A d'accord oui je vois merci à tous les 2 et bonne continuation à vous :lol3:

à 0 car

= = 0

Si le taux d'accroissement à une limite finie quand x tend vers a, on note f'(a) cette limite finie et on dit que f' est dérivable en a

Taux d'accroissement??

c'est indéterminé ...... car c'est de la forme ??

Je vous dérange pour une dernière fois, juste pour que vous me disiez si mon calcul est juste ou pas : f(x)= \frac{x}{2+sin 1/x} Determiner \lim_{x\to +\infty}\left[f(x)-\left(\frac{x}{2}\right)\right] 3)a) f(x)-\frac{x}{2}=\frac{x}{2+\sin\,\frac{1}{x}}-\frac{x}{2}=-\frac{x\,...

f(0)= 0 et
f(1) est environ = à 0.35
mais après, comment je démontre que que les points d'intersection de C (c est la courbe représentative de f dans un repère) et D3: y = x/2 ont tous une abscisse comprise entre 0 et 0.35. ???

Exemple: f(x) = x^3+x-1 on veut prouver l'existence de solutions à l'équation f(x) = 0 et en donner des encadrements f(o) = -1 f(1) = 1 f est continue sur [O,1] car polynomiale Comme 0 appartient à [f(0),f(1)], le TVI prouve l' existence d'au moins une solution pour f(x)=0 sur [0,1] Or dans mon exo,...

D'accord merci. Il y a un autre morceau de l'exo que je n'arrive pas à faire. On me demande de démontrer que les points d'intersection de C (c est la courbe représentative de f dans un repère) et D3: y = x/2 ont tous une abscisse comprise entre 0 et 0.35. Je pense qu'il faut utiliser le TVI mais je ...

Donc j'ai juste à dire que f(0)=0 (Cela donne un fraction de la forme 0/ ... ) Donc lim f(x) = f(0) donc la fonction est continue en 0

C'est bon?

- soit h:x->2+sin1/x
- soit g:x-> x
- soit f: x-> g(x)/h(x) =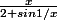 Je retombe sur ma fonction f et je suis pas plus avancé... Qu'est ce que j'ai loupé stp?

- soit h:x->2+sin1/x
- soit g:x-> x
- soit f: x-> g(x)/h(x) = ?

A partir de là je suis largué car je comprend pas la notion de valeur naturelle dans ton exemple

A d'accord merci beaucoup pour cette réponse clair et précise :lol3: Bonne continuation