Il n'y aurais pas du binome de Newton dans cette suite ?
Edit: Oui c'est bien ce que je me disais mais comment trouver le premier terme ? on remplace n par 1 ou bien c'est k que l'on remplace ?
8 résultats trouvés
Revenir à la recherche avancée
- 02 Oct 2010, 08:30
- Forum: ✯✎ Supérieur
- Sujet: [B]Ah toujours des suites de plus en plus compliquées[/B]
- Réponses: 16
- Vues: 1293
- 01 Oct 2010, 07:27
- Forum: ✯✎ Supérieur
- Sujet: [B]Ah toujours des suites de plus en plus compliquées[/B]
- Réponses: 16
- Vues: 1293
ok pas de problème j'espère juste qu'elle ne va pas m'envoyer sur un raisonnement auquel je ne comprendrais rien du tout.
Edit: Busard qu'entends tu de sigma par proche en proche ?
Edit: Busard qu'entends tu de sigma par proche en proche ?
- 30 Sep 2010, 23:03
- Forum: ✯✎ Supérieur
- Sujet: [B]Ah toujours des suites de plus en plus compliquées[/B]
- Réponses: 16
- Vues: 1293
Ah okay...
Bon ben j'aimerais un indice pas trop compliqué pour débuter mais je sais que l'on a vu la récurrence forte récemment donc je penses que c'est ce que je vais devoir utiliser. Je posterais si j'ai des nouvelles idées pour résoudre ce problème mais envoyez moi des pistes de niveau 1 pas trop compliqué...
- 30 Sep 2010, 22:57
- Forum: ✯✎ Supérieur
- Sujet: [B]Ah toujours des suites de plus en plus compliquées[/B]
- Réponses: 16
- Vues: 1293
[B]Ouhla[/B]
C'est quand même bizarre comme formule étant donné que je suis en première année et que je n'ai pas encore vu quoique ce soit d'aussi compliqué, donc je me demande si il n'y a pas plus simple...Je vais quand même essayer mais notre prof n'en attend pas autant je penses.
- 30 Sep 2010, 22:20
- Forum: ✯✎ Supérieur
- Sujet: [B]Ah toujours des suites de plus en plus compliquées[/B]
- Réponses: 16
- Vues: 1293
[B]Ah toujours des suites de plus en plus compliquées[/B]
4. Soit la fonction ) définie par
définie par 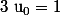 et
et 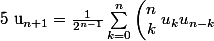 (pour
(pour 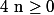 ).
).
Déterminer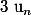
Déterminer
- 30 Sep 2010, 21:54
- Forum: ✯✎ Supérieur
- Sujet: [B]Ah toujours des suites de plus en plus compliquées[/B]
- Réponses: 16
- Vues: 1293
Ah mais d'ou sort cette formule quand meme ?
bon merci je vais essayer ca...
Edit: c'est bon j'ai trouvé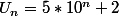
Edit: c'est bon j'ai trouvé
- 30 Sep 2010, 18:58
- Forum: ✯✎ Supérieur
- Sujet: Suite Un a determiner avec U0 et Un+1
- Réponses: 5
- Vues: 14917
Suite Un a determiner avec U0 et Un+1
Bon ben c'est ma première fois donc voila : Un exercice simple mais qui me perturbe un peu parce que je n'ai pas d'informations (elle est comment cette suite ?) : U0=7 Un+1=10Un-18 Déterminer Un. Donc j'ai essayer de voir U1=52 puis U2=502 puis U3=5002...j'ai besoin d'une piste a peu près rigoureuse...
- 30 Sep 2010, 17:23
- Forum: ✯✎ Supérieur
- Sujet: Suite Un a determiner avec U0 et Un+1
- Réponses: 5
- Vues: 14917
- 8 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
