54 résultats trouvés
Revenir à la recherche avancée
J'arrive donc à un truc comme 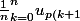}-u_{kp}) qui tend vers u ? Et est-ce qu'à ce moment je peux utiliser directement le télescopage?
qui tend vers u ? Et est-ce qu'à ce moment je peux utiliser directement le télescopage?
- 09 Sep 2012, 14:00
- Forum: ✯✎ Supérieur
- Sujet: Exercice suite, télescopage, convergence MP
- Réponses: 4
- Vues: 1030
- 09 Sep 2012, 12:51
- Forum: ✯✎ Supérieur
- Sujet: Exercice suite, télescopage, convergence MP
- Réponses: 4
- Vues: 1030
Exercice suite, télescopage, convergence MP
Bonjour tout le monde! Alors voilà, j'ai un soucis pour montrer la convergence d'une suite : On suppose qu'il existe un entier naturel p strictement positif tel que v_{n}=u_{np}-u_{n} converge vers une limite u. Montrer en considérant v_{np} que \frac{u_{np}}{np} converge vers u/p Donc je sais bien ...
- 09 Sep 2012, 11:55
- Forum: ✯✎ Supérieur
- Sujet: Exercice suite, télescopage, convergence MP
- Réponses: 4
- Vues: 1030
Salut. Tu peux dire que ln(1+x)=ln(x)+ln(1+1/x). Comme t'en en +l'infini, tu peux faire un dl de ln(1+1/x) comme 1+o(1). Et alors sqrt(ln(1+x))=sqrt(ln(x))*sqrt(1+1/ln(x)+o(1/ln(x)) ce qui te permet de conclure. et en l'infini, on a vraiment pas x équivalent à sqrt(x). Je vois bien que ln(1+x&#...
- 20 Fév 2012, 12:48
- Forum: ✯✎ Supérieur
- Sujet: Recherche d'équivalents...
- Réponses: 3
- Vues: 3549
Recherche d'équivalents...
Bonjour! Voilà mon problème, j'ai un équivalent à déterminer en plus l'infini, d'une fonction pourtant pas bien compliquée, mais malgré tout, je bloque. La fonction est la suivante: f(x)=sqrt(ln(1+x))-sqrt(ln(x)) Pour simplifier le tout, j'ai multiplié par le ...
- 18 Fév 2012, 14:11
- Forum: ✯✎ Supérieur
- Sujet: Recherche d'équivalents...
- Réponses: 3
- Vues: 3549
Etude d'une équation fonctionnelle
Bonjour tout le monde. Voilà j'ai un petit problème pour dériver deux fois une fonction (celle-ci doit vérifier un problème de Cauchy d'ordre 2). Cette fonction est la suivante: pour tout xlR, f(x)=-1- \bigint_{0}^{x} (2x-t)f(t)dt Et je dois démontrer que cette fonction est solution...
- 13 Nov 2011, 11:59
- Forum: ✯✎ Supérieur
- Sujet: Etude d'une équation fonctionnelle
- Réponses: 1
- Vues: 669
Olympus a écrit:Ouép c'est bon alors ! :we:
Et c'est normal qu'il y ait deux solutions pour z? En tout cas merci de l'aide
- 24 Déc 2010, 15:26
- Forum: ✎✎ Lycée
- Sujet: exo nb complexes
- Réponses: 7
- Vues: 548
Re ! Oui là c'est parfait ! Je croyais que t'avais sorti n'importe comment le \Large x\left(x+2\right) mais je me suis trompé désolé :we: ( mais tu t'es quand même un peu gourée ) . Donc t'as le système suivant à résoudre : \Large \left\{ \begin{array}{rel} 2x+x^2+y^2 &=& 33 \\ 2y &...
- 24 Déc 2010, 15:21
- Forum: ✎✎ Lycée
- Sujet: exo nb complexes
- Réponses: 7
- Vues: 548
Bon, tout d'abord je pose z=x+iy et z barre = x-iy Donc l'équation me donne (E): (x+iy)(2+x-iy)=33+6i Je développe ensuite le membre de gauche ce qui me donne (E): 2x+x^2-xiy+2iy+xiy-(iy)^2=33+6i \Longrightarrow(E):2x+x^2+2iy+y^2=33+6i Ensuite j'identi...
- 24 Déc 2010, 15:02
- Forum: ✎✎ Lycée
- Sujet: exo nb complexes
- Réponses: 7
- Vues: 548
exo nb complexes
Bonjour tout le monde. Voici une équation que j'ai du mal à résoudre (E): z(2+z)=33+6i et le deuxième z est un z barre mais je n'ai pas réussi à trouver son symbole. En posant x partie réelle de z et y partie imaginaire de z, j'arrive à x(2+x)=26 car la partie réelle du membr...
- 24 Déc 2010, 12:23
- Forum: ✎✎ Lycée
- Sujet: exo nb complexes
- Réponses: 7
- Vues: 548
- 23 Déc 2010, 19:57
- Forum: ✎✎ Lycée
- Sujet: exercice nombres complexes
- Réponses: 23
- Vues: 1432
- 23 Déc 2010, 19:53
- Forum: ✎✎ Lycée
- Sujet: exercice nombres complexes
- Réponses: 23
- Vues: 1432
Olympus a écrit::hein: :hein: :hein:
Tu ne sais pas différencier ce qui est complexe pur de ce qui est réel ?
Allez j'essaie autre chose maintenant : sachant que les termes réels sont ceux qui n'ont pas de "i" en facteur, retrouve ceux du membre de gauche .
ah donc c'est -x+3y ?
- 23 Déc 2010, 19:40
- Forum: ✎✎ Lycée
- Sujet: exercice nombres complexes
- Réponses: 23
- Vues: 1432
ah bin dans ce cas là je dirais que la partie réelle du membre de gauche est 3y+3x et si c'est pas ça je comprends rien du tout ^^
- 23 Déc 2010, 19:28
- Forum: ✎✎ Lycée
- Sujet: exercice nombres complexes
- Réponses: 23
- Vues: 1432
Olympus a écrit:Non, c'est quoi la partie réelle de?
euh la partie réelle je dirais (-1+3i) et la partie imaginaire (3i+3) ?
- 23 Déc 2010, 18:51
- Forum: ✎✎ Lycée
- Sujet: exercice nombres complexes
- Réponses: 23
- Vues: 1432
Olympus a écrit:Ouép bien sûr :lol3:
En développant j'arrive à
Et donc là j'ai
- 23 Déc 2010, 18:29
- Forum: ✎✎ Lycée
- Sujet: exercice nombres complexes
- Réponses: 23
- Vues: 1432
Olympus a écrit:Euh ...
Retournons à l'équation.
C'est quoi la partie réelle du membre de gauche ? et sa partie imaginaire ?
Bin pour ça il faut développer non?
- 23 Déc 2010, 18:19
- Forum: ✎✎ Lycée
- Sujet: exercice nombres complexes
- Réponses: 23
- Vues: 1432
- 23 Déc 2010, 18:15
- Forum: ✎✎ Lycée
- Sujet: exercice nombres complexes
- Réponses: 23
- Vues: 1432
Bin j'arrive à quelque chose comme ça: : x+yi+23+3i=(2-3i)(x+yi))
Puis à un truc comme ça :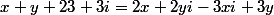
Mais après je sais pas trop trop quoi factoriser, et
et ou juste
ou juste  ?
?
Puis à un truc comme ça :
Mais après je sais pas trop trop quoi factoriser,
- 23 Déc 2010, 18:09
- Forum: ✎✎ Lycée
- Sujet: exercice nombres complexes
- Réponses: 23
- Vues: 1432
- 23 Déc 2010, 17:55
- Forum: ✎✎ Lycée
- Sujet: exercice nombres complexes
- Réponses: 23
- Vues: 1432
- 54 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
