12 résultats trouvés
Revenir à la recherche avancée
D'accord merci
En effet on demandait avant dans l'exercice de montrer que il existait un tel polynôme or (Id,M...M^n) est forcement libre a un moment,
Sinon un autre problème je dois expliciter les suites u et v telles que:
u0=0 et v1=1 vérifiant

et
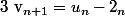
- par Matheur69
- 17 Sep 2010, 12:15
-
- Forum: ✯✎ Supérieur
- Sujet: revisions spé supplémentarité
- Réponses: 30
- Vues: 2106
Mais ca me dit toujours pas comment montrer que M-k*Id n'est pas inversible pour un certain k,
par contre ca solutione ma deuxième question
- par Matheur69
- 17 Sep 2010, 08:59
-
- Forum: ✯✎ Supérieur
- Sujet: revisions spé supplémentarité
- Réponses: 30
- Vues: 2106
Encore un little problem : Il faut montrer que pour toute matrice M de M_n(C) il existe un complexe k tel que M-kId ne soit pas inversible. Je dit que il existe un polynôme P non nul tel que P(M)=0 et que donc avec les a_i racines de P , (M-a_1)...(M-a_n)=0 Mais je ne vois pas comment conclure. Merc...
- par Matheur69
- 16 Sep 2010, 21:09
-
- Forum: ✯✎ Supérieur
- Sujet: revisions spé supplémentarité
- Réponses: 30
- Vues: 2106
oui pardon, c'est E un ev de dimension n et c'est L(E,K) avec donc notre application de K^n dans L(E,K) qui a X associe (Y--> tXY)
C'est donc la surjectivité que j'arrive pas
- par Matheur69
- 16 Sep 2010, 18:20
-
- Forum: ✯✎ Supérieur
- Sujet: revisions spé supplémentarité
- Réponses: 30
- Vues: 2106
Re, j'ai encore un probleme avec ces foutus matrices, on me donne l'application : f : R^n -> L(Mn(K),K) qui a X associe (Y--> tXY) où tX est la trenasose de X. Il me faut montrer que c'est un isomorphisme, sans utiliser les dimensions, je suis donc condamner a montrer que Ker f =0 et qu'elle est sur...
- par Matheur69
- 16 Sep 2010, 12:28
-
- Forum: ✯✎ Supérieur
- Sujet: revisions spé supplémentarité
- Réponses: 30
- Vues: 2106
Ok ok ! Merci beaucoup !
Sinon , j'ai un autre problème, il faut montrer que l'espace des matrices symétriques et l'espaces des antisymétriques est supplémentaire.
MErci
- par Matheur69
- 15 Sep 2010, 18:32
-
- Forum: ✯✎ Supérieur
- Sujet: revisions spé supplémentarité
- Réponses: 30
- Vues: 2106
Ca ok, merci girdav.
J'ai des trous de mémoire et je vois pas pourquoi uniquement grace a cette observation on peut conclure ? Merci de m'eclairer.
- par Matheur69
- 15 Sep 2010, 17:52
-
- Forum: ✯✎ Supérieur
- Sujet: revisions spé supplémentarité
- Réponses: 30
- Vues: 2106
Bonsoir aujourd'hui je suis tombé sur un exercice où l'on me donnait une matrice associées a une application lineaire f et on me demande de calculer le carré de la matrice et d'en déduire que ker f et im f sont supplémentaire sans calculs supplémentaire. Problème je n'y arrive que par la méthode cla...
- par Matheur69
- 15 Sep 2010, 17:03
-
- Forum: ✯✎ Supérieur
- Sujet: revisions spé supplémentarité
- Réponses: 30
- Vues: 2106