Je trouve donc que les deux racines sont
14 résultats trouvés
Revenir à la recherche avancée
- 01 Nov 2010, 10:08
- Forum: ✯✎ Supérieur
- Sujet: Equation du second degré
- Réponses: 6
- Vues: 401
D'accord.
Cette formule magique vient de la forme canonique du polynôme. Donc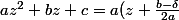(z+\frac{b+\delta}{2a})) avec
avec 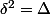 .
.
Ainsi les racines sont et
et  .
.
Le que j'ai trouvé est-il juste ?
que j'ai trouvé est-il juste ?
Cette formule magique vient de la forme canonique du polynôme. Donc
Ainsi les racines sont
Le
- 31 Oct 2010, 14:50
- Forum: ✯✎ Supérieur
- Sujet: Equation du second degré
- Réponses: 6
- Vues: 401
- 31 Oct 2010, 11:20
- Forum: ✯✎ Supérieur
- Sujet: Equation du second degré
- Réponses: 6
- Vues: 401
Equation du second degré
Bonjour, j'ai un souci avec mon dm... On me pose : Résoudre dans C l'équation : z^2-[(3+i)a+4]z+2(3+i)a+4+3ia^2=0 ou a est un complexe donné non nul. On note b et c les deux racines. Je pensé pouvoir calculer delta mais ca ne marche pas. Ensuite j'ai essayé de m'aider d'une condition...
- 31 Oct 2010, 10:26
- Forum: ✯✎ Supérieur
- Sujet: Equation du second degré
- Réponses: 6
- Vues: 401
En refaisant la dérivée je trouve 0, je pense que c'est juste étant donné qu'on a l'égalité au début.
Merci beaucoup
Merci beaucoup
- 10 Oct 2010, 11:07
- Forum: ✯✎ Supérieur
- Sujet: arctan
- Réponses: 10
- Vues: 2237
Merci de bien vouloir m'aider, ca sert à prouver la formule ou à calculer la dérivée la formule trigonometrique ?
- 09 Oct 2010, 11:08
- Forum: ✯✎ Supérieur
- Sujet: arctan
- Réponses: 10
- Vues: 2237
Oui, merci beaucoup. Maintenant je passe à la dérivée. J'arrive à f'(x)=\frac{1}{1+x^2}-\frac{y^2}{(1+xy+x+y)(1-xy)} Je ne sais pas bien si je peu simplifier plus pour arriver à quelque chose de plus agréable pour discuter de la valeur de f, pourriez vous m'indiquer le bo...
- 09 Oct 2010, 10:10
- Forum: ✯✎ Supérieur
- Sujet: arctan
- Réponses: 10
- Vues: 2237
J'ai confondu l'ensemble de définition et les valeurs que prend la fonction. arctan(\frac{x+y}{1-xy}) est définie partout où \frac{x+y}{1-xy} est définie, donc il faut que le dénominateur soit différent de 0 donc xy différent de 1. Et la je ne vois pas bien à quoi x ne doit pas étre égale à cause de...
- 07 Oct 2010, 21:22
- Forum: ✯✎ Supérieur
- Sujet: arctan
- Réponses: 10
- Vues: 2237
arctan
Bonjour, J'ai du mal à faire un exercice, notamment sur le calcul d'un dérivée... Voila l'exercice en question : Le but de cet exercice est de prouver la formule : arctan(x)+arctan(y)=arctan(\frac{x+y}{1-xy})+\left\{ \begin{array} 0 si xy \lt 1 \\ \Pi si xy \gt 1 et x\gt 0\\ ...
- 07 Oct 2010, 20:57
- Forum: ✯✎ Supérieur
- Sujet: arctan
- Réponses: 10
- Vues: 2237
- 12 Sep 2010, 18:22
- Forum: ✯✎ Supérieur
- Sujet: equation de trigo
- Réponses: 12
- Vues: 849
- 12 Sep 2010, 16:30
- Forum: ✯✎ Supérieur
- Sujet: equation de trigo
- Réponses: 12
- Vues: 849
- 12 Sep 2010, 15:39
- Forum: ✯✎ Supérieur
- Sujet: equation de trigo
- Réponses: 12
- Vues: 849
Oui avec la formule sin2x=2*sinx*cosx mais, ensuite j'ai un souci de factorisation... J'arrive à ça : (\frac{2-sqrt(2)}{2})(sin(x)+cos(x))-(\frac{2sin(x)cos(x)}{sqrt(2)+1})=0 Pourriez-vous m'indiquer l'étape suivante ? Merci d'a...
- 12 Sep 2010, 13:40
- Forum: ✯✎ Supérieur
- Sujet: equation de trigo
- Réponses: 12
- Vues: 849
equation de trigo
Bonjour, je commence une année de ptsi, le premier DM est un peu délicat. Il y a une équation trigonométrique que je n'arrive pas à résoudre... Il faut résoudre dans \mathbb{R} l'équation suivante : sin(x)+cos(x)-\frac{sin(2x)}{sqrt(2)+1}=cos(\frac{\Pi}{4}-x) ...
- 12 Sep 2010, 11:38
- Forum: ✯✎ Supérieur
- Sujet: equation de trigo
- Réponses: 12
- Vues: 849
- 14 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
