Forum de Mathématiques: Maths-Forum

Merci beaucoup abcd22, je n'avais pas pensé à chercher sous une autre forme. :happy2:

ce sont les racines de P (les 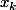) et les racines de P' (les )

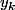sont les n racines de P. On suppose que est racine simple de P.
sont les n-1 racines de P'(polynôme dérivé de P)

Bonjour à tous, voici un exercice qui me pose problème depuis plusieurs jours et que je n'arrive pas à résoudre. P est dans C[X] de degré n x_1,...x_n sont les n racines de P. On suppose que x_1 est racine simple de P. y_2,..,y_n sont les n-1 racines de P'(polynôme dérivé de P). il faut montrer \sum...

merci beaucoup a vous tous

merci
j'avais déja cette égalité, mais je ne comprends pas ce qui nous donne le droit de dire qu'alors a est racine de P.

je suis tout a fait d'accord avec l'initialisation et ce que tu veux faire ensuite en partant de P'. on a P'(x)=(x-a)²(x-b1)(x-b2).....(x-bi) et on veut retrouver la formule P'(x)= (x-a)² u(x) + u'(x) (x-a)^3 pour avoir ensuite P= (x-a)^3 u(x) c'est ca non? seulement je ne ne vois pas comment passer...

Au rang n (avec n entier supérieur à 3), P(x) = C (x-a)^3u(x) polynome de degré n et sa dérivée est ..... j'ai l'impression que tu pars de l'hypothese a racine multiple de P pour montrer a racine de P', alors qu'il faut le faire dans l'autre sens. De plus, je ne vois pas ou ...

non c'est le bon énoncé, c'est justement pour ca que c'est difficile

je ne crois pas qu'il y ait vraiment moyen de faire une récurrence ici, meme en raisonnant sur les differents degrés, mais peut etre vois tu bien comment faire.

Bonjour, j'aimerais avoir de l'aide pour résoudre cette question :

P est scindé sur R. Montrer que toute racine multiple de P' (polynôme dérivé de P) est racine de P.

Merci beaucoup à ceux qui pourront m'éclairer. :happy2: