Forum de Mathématiques: Maths-Forum

C'est lacunaire, on ne peut pas appliquer d'Alembert. Par contre, on peut essayer de revenir à la définition du rayon de convergence : quel est l'ensemble des x tels que la suite \{n!|x|^{n^2}\} soit bornée ? La suite \mid (x)\mid^(n^2) est bornée pour x compris entre -1 et 1 je sup...

Bonsoir à vous

Soit Une Série entière

On a = n! et an = 0 si n =/= 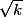avec k dans IN

Comment je détermine le rayon de convergence ? :we: , comment appliquer la règle de d'alembert?

Merci à vous

F et Y vont de R^2 dans R
Je n'ai pas compris comment mesurable --> borélienne ici , je ne connais pas de théorème qui va dans ce sens

Bonsoir à vous On sait que F et Y sont boréliennes et on demande : Expliquer brie;)vement pourquoi G := Y ;) F est bore;)lienne. La réponse est : Y ;) F est mesurable, car l’ensemble des fonctions mesurables a;) valeurs dans R (quel que soit l’espace de de;)part) est un espace vectoriel. Je n'ai pas...

eratos a écrit:c'est quoi une mesure?

http://fr.wikipedia.org/wiki/Th%C3%A9orie_de_la_mesure :we:

Sûrement oui, on m' a jamais enseigné la différence :we:

Donc notre sup Fj ça correspond à quoi finalement? (pardon de spamer et d'abuser de votre pour des choses aussi idiotes :we: )

Salut, pourquoi serait-ce évident? Pourquoi ne le serait-ce pas :we: Mon raisonnement (faux) est très simple et est le suivant : Le sup des Fj est la plus grande mesure parmi les mesures (F1...,Fj....) , donc c'est une mesure : c'est pour moi une tautologie, je n'ai peut être pas compris la notion ...

bonjour à vous :we:

Soit Fj une suite croissante de mesures positives. On demande de montrer que Sup Fj est aussi une mesure. Je ne vois pas ou est le problème , puisque tous les Fj sont des mesures, alors en particulier le sup est... une mesure

Mais le détail du raisonnement c'est quoi ? Manier une tribu c'est pas très naturel pour moi en fait

Un générateur de la tribu borélienne... ? Ce sont les ouverts de R je crois

la partie entière d'un nombre est le premier entier qui lui est inférieur : Ent (3,2) = 3 Donc si ta relation est vraie à partir de 3/esp, elle ne l'est plus pour Ent (3/eps), on prend donc l'entier directement supérieur, cad la partie entière + 1, tu peux évidemment ajouter tout ce que tu veux (+1,...

3/eps n'est pas un entier, on prend donc l'entier directement supérieur pour satisfaire la définition

Bonsoir à vous :we: Je ne comprends rien aux tribus , pouvez vous m'aider : c'est un exercice d'application directe qui ne devrai pas poser de problèmes Soit f :R^2--> R / f(x,y) = x On me demande de décrire la tribu image réciproque de B par f, cad f^-1 (B) = (f^-1 (A), avec A € B) B est la tribu B...

Bonjour à vous :we:

Je comprends mal les notions de lim sup et lim inf : je ne vois pas leur intérêt à part donner un nom à la plus grande et plus petite valeur d'adhérence d'une suite.
Dans quels cas les utilise-t-on ?

Nightmare a écrit:Ce n'est pas important. Ce qu'on sait c'est que si X < B alors f(X) < c.

Ca donne quoi en prenant X=d(x,x0) ?

ça nous donne ce qu'on veut, j'ai compris le truc merci :we:

Nightmare a écrit:Rien à voir entre elles? Pourtant l'une est l'image de l'autre par f, c'est pas rien...

Non je parlais de la relation entre la distance usuelle et ces deux distance d et D :we:

Joyeux noël à vous :we: Soit (X,d) et (X,D) deux espaces métriques. f une fonction croissante de R+ dans R On définit D par D(x,y) = f (d(x,y)). On sait que f est continue en 0 On me demande de montrer que Id : (X,d)-->(X,D) est continue,ainsi que son inverse Le corrigé donne : f continue en 0, d'où...

Bonjour à vous :we:

On me demande de déterminer l'image du plan P = ( l' ensemble des z / Imz>0)

Par la fonction définie dans C par

Comment feriez vous ? :we:

cuati a écrit:Bonjour,
c'est l'application directe de l'inégalité de Cauchy Schwartz avec les vecteurs et et le produit scalaire usuel...

EN effet :we:

Bonjour à vous , d'ou vient il que <= ).

Comment ce résultat est il obtenu?
Merci