Forum de Mathématiques: Maths-Forum

Quand u tend vers 0 u ln(u) tend vers 0
Donc e^(u ln(u))-1 équivaut à u ln(u), avec u(x)=sin(x).
Comme u(x) équivaut à x, un bon équivalent est x ln(sin(x)).

En supposant que rg (A)>1 et Aij>0: quitte à permuter les colonnes et les lignes ce qui ne change rien (ni au rg ni aux hypothèses sur les coefficients), on peut supposer que les deux premières colonnes engendrent un plan, et même que les quatre coefficients A11, A12, A21 et A22 forment une matrice ...

En résolvant l'équation 0 = (A B, C D) * (I 0, 0 0) - (I 0, 0 0) * (A B, C D) (les inconnues étant les blocs A B C et D) on doit tomber sur ce que tu as trouvé (ie B=0, C=0). Ensuite, la dimension de l'espace des solutions est la somme "taille de A" + "taille de D" c'est à dire r²+(n-r)² qui a même ...

Ok je n'avais pas vu que l'on pouvait voir le lien comme ça dibeteriou ! Du coup A= Ir 0 0 0 et l'on cherche les B qui commutent avec A, on va pouvoir les déterminer ces matrices ou juste la dimension ? PS. Evidemment la méthode de FF m'intéresse aussi :lol3: On peut déterminer les matrices entière...

Bon j'ai pas tout lu dans les derniers messages, mais tu dois savoir que A est une symétrie, donc s'écrit A=I-2p où p est le projecteur parallèlement aux points fixes, sur les points changés en leur opposé. M commute avec A ssi M commute avec p (pourquoi ?). La matrice de p est une matrice Jr (diago...

C'est pourtant le plus simple à mon avis : écrire la matrice dans une base sympa et faire des calculs par blocs (ce qui revient à faire de la réduction sans le dire).

Bonne année :)

Euh on la refait : Tu prends ta matrice A ok, et B inversible ( GL_n(R) ) et bien B+xA sera même inversible pour x dans un intervalle centré sur 0 , mais faut le prendre suffisemment petit l'intervalle. [tu as écrit A+xB qui change ... tout ] Pour la preuve ... on voit ça plus tard dans la journée ...

Salut Voila je bloque sur un théorème dans mon cour qui stipule que : si deux matrices sont semblables alors une de ces matrices est égale a la matrice de l'endomorphisme canoniquement associé a l'autre matrice dans une autre base ... ou encore : B =P^{-1}AP \Longrightarrow \exists b , une base, te...

Ouais je vois le problème... il faut dire qu'en prépa, on admet que toute application linéaire définie sur un espace de dimension finie est continue :we:

Salut,
En dimension finie :
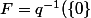soit un projecteur sur un supplémentaire parallèlement à . où est continue car linéaire. est donc fermé.

J'ai l'impression que j'ai également loupé la solution ce matin :mur:
A suivre...

On pose S_n=\bigsum_{q=1}^{n} a_q . Par hypothèse : O(1)=S_n-n(S_n-S_{n-1})=nS_{n-1}-(n-1)S_n donc O({1\over n^2})={S_{n-1}\over n-1}-{S_{n}\over n} donc ({S_{n}\over n}) a une limite L . Il reste deux lignes à écrire... (mais j'ai mis deux heures à le voir !)

Bon alors pour prouver que A est dense dans R, on va prendre x\in R et montrer que pour tout \epsilon>0 x est approché par un élément de A à \epsilon près. Soit donc \epsilon>0 fixé. Il existe deux éléments a et b de A tels que a<x<b. Désormais la deuxième propriété ne va plus servir (attention à la...

Attention à ne pas confondre égalité (entre expressions algébriques) et équivalence (entre phrases logiques) !

Il faut utiliser la propriété :
(on fait des permutations circulaires des trois vecteurs), que tu as peut-être vu en cours.

Le déterminant vaut :
*-* ce qui fait penser au membre de droite de la première égalité...

*-*=*d-*c)>==produit mixte de [b,a,d^c]=...

C'est pas la question, qui est : on place p frontières, de combien de façons différentes peut-on le faire?

Autre méthode, qu'on rencontre souvent :
on pose et on cherche P tel que ...

Il y a un problème classique qui répond presque à ta question :
On considère n points alignés. Comment placer p frontières entre ces n points de sorte qu'entre deux barres il y ait toujours au moins un point ?