Forum de Mathématiques: Maths-Forum

Merci beaucoup pour ton aide !
Je trouve 1 comme limite en 0+ c'est bien ça ?

Bonjour, Je cherche à calculer avec des outils de TS (donc equivalents et DL exclus) cette limite : \lim_{x\to 0}\frac{\sin^{x}x-1}{x^x-1} J'ai essayé de transformer l'expression en \frac{(sin{x}-1)\bigsum_{k=0}^{x-1}sin^{k}x}{(x-1)\bigsum_{k=0}^{x-1}x^k} , sachant que \frac{\sin{x}-...

Merci je comprends beaucoup mieux maintenant !

D'accord je crois que je comprends mieux...
Mais quelle est la méthode pour pour déterminer un équivalent au voisinage d'un point ?

Ce que je ne comprends pas, c'est que si on s'en tient au simple fait que cos(0)=1, la limite du numérateur revient à la limite de 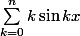en 0 qui est 0*0+1*0+2*0+...+n*0=0

Or, le résultat attendu n'est pas du tout le même...

Chacun des sin(kx) est équivalent à kx

Mais que veut dire "equivalent" exactement ?
On ne voit pas vraiment cette notion au lycée pour calculer des limites si ?

Rebonjour, Désolé, je suis un boulet je sais, mais pour revenir sur un des lien qu'a posté Ericovitchi, je ne comprends pas ce calcul : f' (x) = sin(x)cos(2x) ..cos(nx) + cos(x)2sin(2x)...cos(nx) +... +cos(x)cos(2x)...nsin(nx) Un équivalent de f' (x) est donc: ( 1² + 2² +... + n² ) * x Quand il parl...

Ah oui je suis c** ! Merci beaucoup :)

Sa Majesté a écrit:
Et

J'imagine que c'était

Mais c'est justement ça que je ne comprends pas...

Sur ce site ils parlent d'une méthode qui n'utilise pas la règle de l'hospital mais je ne comprends pas la dernière étape quand ils passent de l'expression de la limite à

Merci beaucoup de ta réponse !
Je ne suis qu'en terminale, je n'ai pas encore vu les développements limités. Je vais essayer avec la règle de l'Hospital...

svp... :hein:

Pour la première j'ai un peu simplifié l'expression, je sais pas si ça peut aider :

J'ai :

Bonjour, j'ai deux limites que je ne sais pas trop comment déterminer. Merci de m'aider svp

1ère :


2ème :

Désolé Ericovitchi c'est parce que j'essaye d'avoir le plus de réponses possibles...

Sinon merci pour le lien Rebelle!

Personne ?

Bonjour, Je bloque sur cet exercice, un peu d'aide serait bienvenue :) On a u_0=0 et u_{n+1}=\sqrt{12-u_n} Je dois montrer que \forall n\in\mathbb{N},|u_{n+1}-3|\leq\frac{1}{3}|u_n-3| , en déduire que \forall n\in\mathbb{N}*,|u_{n}-3|\leq\frac{1}{3^{n-1}} , puis conclure sur la convergence de la sui...

Bonjour, Je dois étudier la convergence de la suite réelle définie par \huge u_0\geq 0 et \huge\forall n\in\mathbb{N}, u_{n+1}=\sqrt{u_n}+\frac{1}{n+1} Je ne sais pas vraiment comment aborder l'exo. J'ai pensé à montrer que la suite était à termes positifs, pour montrer ensuite qu'elle est décroissa...

Ok merci! :)

Bon je sais pas pourquoi je me suis compliqué la vie lol en fait c'est tout simple : 1)a) On a : \huge 0\leq k\leq 2n+1\\n^2\leq n^2+k\leq n^2+2n+1\\ \frac{1}{(n+1)^2}\leq \frac{1}{n^2+k}\leq \frac{1}{n^2} 1)b) La somme est composée de \huge 2n+2 termes, on multiplie de chaque côté : \huge\f...