Forum de Mathématiques: Maths-Forum

Très juste, définie sur dans . :dodo:
J'ai justement fait l'erreur à laquelle je demandais de prêter attention : échec & mat :soupir2:

Au passage, 4$ \sqrt{4} = 2 (Sans le -2) D'après mon cours..! Je n'ai jamais vu ça de ma vie dans un cours, à part si c'est précisé : l'une des racines de 4 est 2, sinon cela voudrait dire que 4$ \sqrt{4} n'a qu'un seul et unique antécédent et c'est faux. Mais j'ai néanmoins déjà écrit 4$ \sqrt{x} ...

je tient a signaler que la méthode de friandise est sensiblement la même que la mienne, et que bien que ce soit réellement une solution vectorielle, comme l'a signalé ben, on a TOUS la même méthode ici, puisque on s'est servi d'une base. En effet, on va dire que j'y ai mis une meilleure présentatio...

Ok, bon ben je mets ce que j'avais évoqué avant, solution purement vectorielle. Je mets toutes les étapes pour ne pas se perdre... Nous avons : \vec{AM} = k\vec{AB} \Longleftrightarrow \vec{MA} = k\vec{BA} \vec{BN} = k\vec{BC} \Longleftrightarrow \vec{NB} = k\vec{CB} \vec{AI} = \frac{1}{2}\vec{AB} \...

En effet, je n'ai pas prêté attention au .

Voici le LaTeX

Valeur absolue, module... ?
Peux-tu utiliser LaTeX pour nous montrer ça ?

Merci d'enlever la réponse, nous ne sommes pas là pour résoudre les exercices des autres, mais de les aider à les résoudre eux-même.

Ben en fait, Magritte a peint ce tableau pour démontrer le danger des associations d'idées. Même la plus représentative possible, une image de pipe n'est pas une pipe. Ca ne reste qu'une image... Le danger ? C'est là où se trouve l'intelligibilité et l'intelligence humaine, et même animale. Quand q...

on n'a pas le droit à Thalès lorsqu'on utilise les vecteurs? Ou faire du Thalès sans le dire? Le théorème de Thalès vectoriel : Soit ABC un triangle quelconque et les points M et N tels que, \vec{AM} = k\vec{AB} et \vec{AN} = k\vec{AC} , nous avons alors \vec{MN} = k\vec{BC} . Mais où veux-tu donc ...

6$ \sqrt{4} = 4$ \sqrt {(-2)^2} Peut-on se permettre de poser 4$ \sqrt{4} = -2 ? Je ne pense pas, car ça va à l'encontre de la définition de la notation.. :doh: C'est faux, il faut écrire \sqrt{4} = 2 ou -2 . C'est les deux valeurs et non pas une seule. La fonction \sqrt{x} n'est tout simpl...

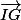
Si, il faut essayer d'exprimer en fonction de .

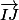
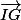
Transforme l'écriture de jusqu'à ce que tu tombes sur

Vu en spé : une équation d'un cône de révolution d'axe



étant l'angle formé entre une génératrice du cône et l'axe du cône.

Tu veux parler de la linéarité des intégrales ? C'est une propriété vue en cours normalement non ?

Oui, c'est ce que j'ai fait... En fait, j'avais mal lu l'énoncé, je travaillais avec un \alpha = \frac{1-e}{2e} et je n'arrivais pas à me débarrasser de la racine... :mur: (1) u(\alpha) = sqrt{\left( \frac{1-e^2}{2e} \right)^2+1}-\frac{1-e^2}{2e} (2) u(\alpha)...

Bonsoir à tous, Est-ce que quelqu'un ici peut me mettre sur la voie pour : Soit u la fonction définie sur \mathbb{R} par u(x) = sqrt{x^2+1} - x Soit \alpha = \frac{1-e^2}{2e} , montrer que u(\alpha) = e . J'ai le cerveau en compote, alors ne soyez pas trop durs :triste: Merci d'avanc...