Forum de Mathématiques: Maths-Forum

En tout cas je remercie car j'ai réussit
à bientôt

haydenstrauss a écrit:C'était quoi ton erreur ?


( va falloir que je fasse attention au fautes lol )

Ma faute n'a pas d'importance! Vous m'avez fait tourner en rond pendant toute l'aprème-midi! Je veux savoir tout simplement comment faut-il faire pour démontrer que
Merci

haydenstrauss a écrit:hum

sa donne pas zero

Non mais c'est moi qui a tout faux! Je me suis cassé la tête toute l'après midi et ça n'a servi à rien!

ouais y'a un probleme la \frac{\phi ^2}{\phi} = \frac{\phi + 1}{\phi} donc \phi = \frac{\phi}{\phi}+ \frac{1}{\phi} Pour trouver \phi = 1 Ensuite j'ai pris le premier membre et je l'ai simplifier ce qui fait \phi et ensuite au 2ème membre j'ai aussi simplifier en barrant les \phi ce qui me fait 1! ...

Les réponses te disent de diviser la première égalité par phi. Si tu sais faire une division tu devrais réussir. Sinon relis les réponses. Oui je sais j'ai bien compris , il faut que je divise les membre de cette égalité \phi ^2 = \phi + 1 \mbox{ par \phi et de chaque cote.} Mais quand je l'ai fait...

:triste: Non je trouve pas! Je trouve =1

Je vais être clair : J'ai beau relire vos réponses mais Je ne comprend rien du tout! DéSoLé

Sinon besoindaide tu as compris ? tu prend ton eqaution : \phi ^2 = \phi + 1 \mbox{ et tu divises par \phi de chaque cote.} Cet équation la \phi^2 = \phi +1 je l'ai déjà fait. Celle que je n'arrive pas c'est celle-la \frac{1}{\phi} = \phi -1 Est-ce que tout dabord je dois y remplacer par les valeur...

ok merci beaucoup de m'avoir consacré du temps! :we: Je vais essayer de comprendre...

nox a écrit:eh bien essayes de diviser les 2 membres de ton équation par

Vous en êtes sûr que je dois diviser ces 2 nombre par ? Je comprend pas pourquoi? On parle de la même chose? Moi je veut montrer que
= -1

Non je suis votre travail car je fais le même devoir que Noémie!:ptdr:

Oui je voulais dire = +1 :langue:
Comment ça diviser par

Alors si je comprend bien pour démontrer que est la solution de l'équation : x²-x-1=0 , il faute que je résoud cette équation la :
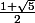- -1=0

Pour démontrer il faut que je fasse cela?

Merci Nekros de m'avoie aider pour celle ci
=
Mais maintnant je bute sur celle-ci!
= -1

Et comment démontre que est solution de l'équation : x²-x-1=0 ... je cherche avec mon père depuis un moment! Merci

Quelle logique! Merci beaucoup!

Et pour le deux est-ce que quelqu'un pourrais m'aider?

Dacord merci!

Mais peut-on encore continuer?

Je bloque à
Je ne c'est pas comment faire ici! Peut-être que j'ai mal fait mes calculs?

Merci de m'avoir montrer un indice! Je travaille à fond la!