Forum de Mathématiques: Maths-Forum

C'est vrai que ça n'a pas de sens de recoller les billets n'importe comment mais bon c'est l'énoncé...

Merci beaucoup Ben pour ta réponse, je n'aurais pas pensé aux partitions par paire.

On accepte A1+B1 et A2+B2 (même si l'énoncé précise qu'il y a des morceaux droits et morceaux gauches), puisque la question suivante est : quelle est la probabilité qu'un morceau gauche soit recollé avec un morceau droit ? Je sais que pour la deuxième question il faut calculer le nombre de bijection...

Bonjour, J'ai encore un petit problème de dénombrement. Si on dispose de n billets de banque que l'on décide de couper en deux. On les recolle deux à deux. Quelle est la probabilité de tous les recoller dans l'ordre initial ? Je n'arrive pas à trouver le nombre d'arrangement total. Pour n=2, je trou...

Merci Ben pour tes explications !

Donc si je ne me trompe pas :

P( 3 filles | au moins 2 filles)=P(3 filles)/P(au moins 2 filles)

avec P(3 filles)=816/4060 et P(au moins 2 filles)=1 -P(0 filles)-P(1 fille)=1-220/4060-(66*18)/4060

Bonjour ! Je sèche sur un problème tout bête : une classe comporte 18 filles et 12 garçons. On tire au hasard un échantillon de 3 élèves sans remise. Sachant que cet échantillon contient au moins deux filles, quelle est la probabilité d'avoir 3 filles ? Ce qui me dérange c'est de ne pas savoir s'il ...

bonsoir

si p est une endomorphisme qui commute avec avec q un endomorphisme normal (ie q.q*=q*.q), montrer que p commute aussi avec q*.
je dois donc montrer que pq*=q*p mais j'ai beau retourner dans tous les sens , je n'ai pas réussi à démontrer l'égalité....

Ok merci Arnaud.
Ca marche bien puisque je travaille dans R.
Je me demande quand même si on peut trouver des conditions necessaires et suffisantes sur M pour avoir M+M*=0 <=> M=0, dans le cas où M est une matrice a coeff réels....

en y reflechissant, je crois avoir dit n'importe quoi, u*ATB*v appartient à R.....donc si je montre que u*ATB*v et v*BTA*u sont tous les deux strictement positifs, alors forcément u*ATB*v=0 et v*BTA*u=0. Mais comme v*BTA*u = (u*ATB*v)*, cela équivaut à u*ATB*v=0. Est-ce correct?

Eh bien pour la diagonale de M je ne vois pas trop quels sont les éléments....A part qu'il faut qu'ils ne soient pas tous nuls pour que ça marche....

Bonjour, Soit T une matrice symétrique, A et B des matrices d'ordre (m,n) et (k,n). u un vecteur de R^m et v un vecteur de R^k. Je note u* le vecteur transposé. A le fin d'un raisonnement, j'aboutis à l'équivalence suivante : u*ATB*v + v*BTA*u =0 <=> u*ATB*v = 0. Le sens <= me parait completement év...

Merci beaucoup à tous!

Arnaud, je ne vois pas pourquoi on utilise (n+1)^3....? Je veux sommer (n-i)^2 pour i de 0 à n-1......

pour la variance, j'ai \sum_{i=0}^{n-1} (n-i)^2 = \sum_i n^2 + \sum_i i^2 -2 \sum_i ni = n^3 + .....- n^2(n-1) , je ne me souviens plus de la somme des i^2...mais je sais que c'est quelque chose équivalent à n^3 en l 'infini, au final j'ai donc ma variance qui équivaut à 1. Ma gaussi...

hmmmm, désolée! Il s'agit de var centrée réduites.....autant pour moi! Du coup la moyenne tend vers 0. Par contre pour la variance, j'ai \frac{1}{n^3} \sum_{i=0}^{n}(n-i)^2 qui doit se simplifier mais comment..... Pour établir la convergence en loi, est-ce correct d'étudier seulement la conv...

Ok, merci....je vois. Mais je reste quand même convaincue qu'il existe une solution à cet exercice, je l'ai trouvé dans quasiment tous les cours de probas niveau M1/prépa agreg.....malheureusement je n'ai pas la correction.

Mettre tout sur le même dénominateur, je veux bien mais ca me donne quelque chose qui ne se simplifie pas.....
la moyenne vaut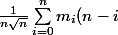 mais ça ne m'avance pas vraiment :triste:

Bonsoir, un exo classique : Soient X_1,X_2,....X_n des v.a indépendantes de loi gaussienne oùX_i suit une loi normale : N(m_i, \sigma _i^2) On veut étudier la convergence en loi de S_n=\frac {nX_1+(n-1)X_2+.......+X_n}{n \sqrt n} J'ai simplement fait la somme des espérances et la som...

Bonsoir, est ce que A= [1,2] \cup ( \cup_{n\ge 1} \left\{\frac{1}{n}\right \}) est fermé dans R? ouvert dans R? En fait, je voudrais savoir si mon raisonnement tient la route : Pour ouvert, je dirais non car [1,2] n'est pas ouvert. Pour fermé, je prends le complémentaire ]-\infty,1[ \cup ]2,...

Je me réponds à moi même, je pense avoir compris, en fait si 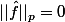ça signifie que 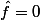presque partout et donc bah c'est la classe du zéro dans 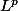et donc c'est fini^^.

ok merci, je ne suis pas du tout à l'aise avec ces nouvelles notions. J'ai une autre question.... si je prends f dans \cal {L^p} et \hat {f} un représentant de sa classe d'équivalence dans L^p je voudrais comprendre en quoi L^p est normé, on veut démontrer que si ||\hat{f}||_p = 0 alors \hat{f}=0 , ...