Forum de Mathématiques: Maths-Forum

Effectivement f doit juste être dérivable continuellement n fois.

Quand est il pour l'équation générale ?

adrien69 a écrit:Sinon, pour f=0 ça marche ^^

Bien tenté mais ca ne donne pas d'équation différentielle. (elle serait dégénérée)
tu dois avoir mini deux des paramètres de f apparaissant dans l'équation.

Salut ! Avant tout chose, je désigne ce problème comme très complexe et ferait peut être appel à d'outils puissants (?) de l'analyse. soit y une fonction différentiable (de classe C^{n} }) (disons sur un certain intervalle I). y est il solution d'une équation différentielle (peu importe son genre et...

C'est bien la définition de la croissance d'une fonction. Ta fonction n'est pas croissante. Le fait que la dérivée soit strictement positive est une condition loin d'être suffisante pour conclure. Par la suite fais très attention quand tu dérives. Il est interdit de dériver une fonction avant de sa...

Salut, il y a un théorème qui s'appelle le théorème de la bijection qui peut répondre à ta question ! Il dit que si une fonction est strictement monotone elle est bijective (ou injective selon l'intervalle d'arrivée) mais l'injectivité suffit à répondre que non. La définition de strictement croissa...

Je dis non. Dès lors que la fonction a dépassé 0 strictement elle ne peut plus y revenir. Donc le seul moyen d'avoir une infinité de 0 serait qu'elle s'annule sur tout un intervalle non réduit à un point. Mais cela est impossible par définition de "strictement croissante" C'est quoi ta dé...

sylvain.s a écrit:Je dirais que la fonction puissance 10 pourrait faire l'affaire, f(x)= 10^x

Sa limite en + infini, c'est un 10 avec une infinité de 0 derrière

Mais je sais pas si j'ai bien compris la question^^

je veut dire une infinité de réels x tel que f(x) = 0

Salut,
voici un problème assez sympa : Existe t'il une fonction f strictement croissante définie dans admettant une infinité de zéro ?
merci à ceux qui voudront répondre.

Ce que j'ai fait est vrai dans le cas quand f(x) est négatif ca reste à voir

Bonjour, Je viens ici car j'ai un exercice dans lequel je dois résoudre 5 équations trigonométriques mais je suis incapable de les résoudres ... Pourriez-vous m'aider en me mettant sur la voie ? 1) cos (3x-\frac{\Pi}{4}) = cos (x+\frac{\Pi}{3}) 2) 2sin (x-\frac{\Pi}{4}) -1 =...

Comment le dit bien Dinozzo13, on arrive dans le cas de l'égalité l'équation f(x)=\frac{1}{f(x)}+\frac{1}{f(0)} , en posant f(0)=\sqrt{2} on a f(x)=\frac{1}{f(x)}+\frac{1}{\sqrt{2}} et en simplifiant le dénominateur f(x)=\frac{1}{f(x)}+...

trouvé les fonctions 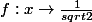et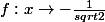
il semble qu'il n'y a que des solutions constantes dans le cas de l'égalité... ( montré par l'absurde )

Salut
Je vois que je t'ai inspiré.. :zen:
g doit être continue sur R ?

Judoboy a écrit:Ah bah oui si tu poses f(x)=x ça va vite c'est sur, mais tu rates probablement quelques solutions.

dans le cas de l'inégalité stricte j'obtiens un encadrement de f(x) qui ne peut être "agrandi" donc bon...

ma solution est surement fausse, j'ai supposé que f(x) est de la forme f(x) = x pour arriver à une inéquation du second degré et la suite en découle... ( deux familles de fonctions dont l'une est bornée, l'autre majorée )

Merci de la réponse !
On peut même dire que f(x) est de signe constant ( th des valeurs intermédiaires )
edit : j'pense avoir résolu entierement le problème, c'est pas aussi difficile que ca en fait

Salut ! Soit f une fonction définie, continue et à valeurs dans \mathbb{R} Il faut déterminer l'ensemble des fonctions qui satisfaissent à l'inégalité suivante : f(x+y) \le \frac{f(x)+f(y)}{f(x)f(y)} et ce pour tout réels x et y. Bon courage. ( pour info j'ai ...

la fonction convient, reste à voir si c'est la seule ou non.

Iroh a écrit:La fonction constante qui vaut 1 ?

Effectivement, et si on vire le -1 ?