Forum de Mathématiques: Maths-Forum

Ok !

Bon ben merci bien pour toutes tes réponses, ça m'a été très utile !

:++:

Oui effectivement, y'a un truc que je doit pas capter...

Ta phrase : "il faut remplacer les matrices par leur application linéaire associées", je pense que c'est la base du problème.

Et bien c'est ça que je comprend pas. :triste:

Ok.

Donc si je résume, la solution c'est :

f admet toutes les solutions telles que :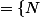 tel que tel que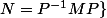

et tq : N.N = -Id

C'est ça ?

Pour P, on doit prendre :

P= a b c d
e f g h
i j k l
m n o p

?

Ou alors je dois trouver toutes les matrices tq M.M = -Id(R^4) ?

Je patauge ...

Il n'y a donc qu'une seule solution pour f.

Et dans ce cas là, on doit avoir un P bien particulier non ?

Oui, c'est bien "Déterminer f appartenant à End(R^4) tq fof = -Id (R^4)"

Si on peut prendre P quelconque (unique condition : P inversible), alors si on prend :
P = 1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

ça marche non ?

Ou alors j'ai pas compris...

PS : je pense que c'est la 2ème option ! :help:

On peut donc prendre P = base canonique ?

Oui, mais dans ce cas là, que vaut P ? Ça me bloque.

Je ne comprends pas bien.

Il faut que j'utilise : M(f,R^4)=P(-1).M(f,B).P ?

Est-il correct alors de conclure que f(x) = M.x pour la question d) ?

Est-il juste de faire ceci :

fof = M.M =
-1 0 0 0 = -Id(R^4)
0 -1 0 0
0 0 -1 0
0 0 0 -1

Donc f=M

?

Help !

Après, j'avais 2 autres questions.

c) Trouver la matrice de f dans B
d) Déterminer f appartenant à End(R^4) tq fof = -Id (R^4)

Pour c) : j'ai trouvé
M = 0 -1 0 0
1 0 0 0
0 0 0 -1
0 0 1 0

Pour d) Faut-il partir de : fo(f^-1) = Id, ou pas ?

Après, j'avais 2 autres questions.

c) Trouver la matrice de f dans B
d) Déterminer f appartenant à End(R^4) tq fof = -Id (R^4)

Pour c) : j'ai trouvé
M = 0 -1 0 0
1 0 0 0
0 0 0 -1
0 0 1 0

Pour d) Peut-on partir de : fo(f^-1) = Id, ou pas ?

Ah ok !

Merci bien Arnaud ! En fait, je comprenais pas le terme "appliquer f".

Merci Arnaud pour ta réponse sur la question b. J'ai tout compris ! :id:

Par contre, pour le a), je suis vraiment en lutte. :mur:

Quand tu dis "tu appliques f à l'égalité (c'est la qu'intervient le fof = -Id)",
je dois reprendre le truc de Nightmare, en disant que fof(x) = k².x ?

J'ai vu sur d'autres forums que fof(x) = -Id(F) revient à fof(x) = -x

C'est ça ?

Id(F), c'est la matrice identité non ?

fof(x) = k².x = -Id (F)

Donc x=-1/k².Id (F)

Dans ce cas, on aurait donc : fof(x) = k².x

Mais après, faut-il déterminer la famille libre avec x et f(x) = k².x ?