Forum de Mathématiques: Maths-Forum

Bonjour,

J'ai bien essayé de montrer que cos(n) est un polynôme en cos(), mais je n'arrive pas, pouvez-vous m'aider???

Et merci.

OK, très grand merci.

Et après avoir trouvé l'équation paramétrique comment montrer que c'est un espace vectoriel???

Chacun des deux ensembles représente une droite, le point d'intersection est:
la solution de l'équation x+2y-z=x+y+z y=2z, mais je ne vois pas la solution???

Bonjour,

E={}
F={}

On doit montrer que (E F,+,.) est un espace vectoriel réel.
Pouvez-vous m'aider à déterminer premièrement l'intersection??

OUI, vous avez totalement raison, merci.

Bonsoir,

comment montrer que: = 0 =0 (, x R)

Et merci.

Bonsoir,

Soit n et A l'ensemble des polynômes. Je dois montrer que la partie suivante n'est pas un sous-espace vectoriel de A:

A/ d°p=n}, tel que d°p est le degré du polynôme p, je sais que je dois montrer qu'il existe un polynôme q tel que p+q , mais lequel

comment avez-vous montré que ???

Bonjour,

Soit (F();+;.) un espace vectoriel réel;

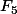
Est-ce-que : ={f F( } / f(0)=f(1) est un sous-espace vectoriel ou non???

Bonjour, Dans un espace vectoriel de dimension 3, on considère une base B_1=(\vec{u_1} , \vec{u_2},\vec{u_3}) et la famille B_2=(\vec{e_1},\vec{e_2},\vec{e_3}) tel que : http://ups.imagup.com/09/1271997947.jpg Je dois montrer que B_2 est une base dans E: j'ai su montrer que B_2 est l...

Ok grand merci.

Bonjour, Je sais bien que pour montrer que des vecteurs sont linéairement indépendants il suffit d'écrire leurs coefficients sous forme de matrices, et d'essayer d'extraire une sous-matrice carrée de déterminant non nul. Ma question est que faire si la matrice est carrée(nombre de lignes = nombre de...

Pour la 2)- (+).(x;y)=( x + x; y + y), est ce que c'est juste???

Bonsoir, \mathbb{R}^2 est munie de la loi interne + et externe . Je dois déterminer dans chaque cas si ( \mathbb{R}^2 ,+, . ) est un espace vectoriel réel: 1)- (x,y)+(x',y')=(x+x';y+y') \alpha .(x;y)=( \alpha x;y) 2)- (x,y)+(x',y')=(x+x';y+y'+2) \alpha .(x;y)=( \alpha x; \alpha y) Il est clair que (...

Bonjour,

J'ai une question qui me dérange bien, quelles sont les applications concrètes de l'algèbre dans notre vie quotidienne, et quel est le but de son étude ????

Et merci.

Bonsoir,

De plus .

Mais vous n'avez-pas trouvé (z)=1???

Je n'ai pas bien compris, pouvez-vous mieux éclaircir si vous le permettez???

Bonjour, On considère A={a+i/(a,b) \in \mathbb{Z}^2 } On considère l'application: A \Longrightarrow \mathbb{Z} \ \ z=a+ib \Longrightarrow \phi(z) = \sqrt{a^2+b^2} J'ai montré que \phi est un homomorphisme de (A,x) vers( \mathbb{Z} ,x), mais je ne sais pas comment montrer l'équivalence suivan...