Forum de Mathématiques: Maths-Forum

Je suis d'accord sur le fait que les maths ne soient pas méthodiques. ^_^ Mais si la proposition n'est pas vraie pour x > n,cela n'implique pas que la proposition l'est pour x=< n Enfin,on va conclure sur un exemple et vous allez me dire très grossièrement ce qu'il en retourne. ^_^ e.g : \forall n\i...

Cela a aussi été une idée,mais j'ai peur de ne pas pouvoir faire une généralisation à tout n de N* après...

Bonjour à toutes et à tous. :) J'aimerais simplement comprendre le principe d'une démonstration ou l'intituté est du type : "Quelque soit n entier strictement positif, et quelque soit x appartenant au fermé [0,n], MQ P(n,x)" (Quelle que soit la proposition évidemment...) J'ai pensé à une récurrence ...

Bonsoir à toutes et à tous. Voici un problème posé par mon professeur de mathématique il y a quelques temps,je l'ai trouvé pas mal et je voudrais vous en faire profiter : Dans un Wagon de chemin de fer se trouvent de vieilles ladies très dignes.Le contrôleur signale : "Certaines d'entre vous on...

Bonjour à toutes et à tous,pourriez-vous répondre à une question concernant la résolution d'une équa diff:

Quelle serait une des primitives de la fonction :

Merci

En fait,ce que tu dis est tout à fait juste,je cherche la complication depuis tout à l'heure,mais je vais prendre ca comme démonstration..

Merci à toi ;-)

A+,cordialement Gauthier.

Si bien sûr,mais étant donné que j'ai cet exercice en devoir maison,que je ne comprend pas bien les démonstrations à faire et que ca me stresse de ne pas comprendre,je suis allé sur le site Wikipedia pour avoir une explication claire et précise,or elle ne l'était pas ,car il catapulte un résultat et...

Encore une question (Genre le lourd -_-)amis mathématiciens. Dans toutes les pages que je lis,il y a les même résultats, \Delta > 0 \Longrightarrow il existe une solution réelle z=u+v et il existe deux autres solutions complexes conjuguées telles que : z_2= \quad \bar {j}u + jv et z_3=ju+\quad \bar{...

Merci beaucoup à vous.
J'avoue Tize que c'est marrant car je feuilletais exactement la même page au moment de lire ton message ^_^. :ptdr:

Voilà encore merci pour vos liens ;-)

A+,cordialement Gauthier.

Bonjour
N'"y aurait-il personne pour confirmer ou infirmer ce que j'avance et m'aider à répondre aux deux dernières questions pour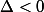 et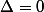

Merci d'avance

C'est moi :),Merci pour le théorème d'Alembert,ca peut servir partout ;-).
Par contre les démos,j'avoue ne pas les avoir comprises ,va falloir que je les relise .

A+,cordialement Gauthier.

Rebonsoir :) Alors pour la méthode: On a : \Delta > 0 \Longrightarrow \exists (U,V)\in\mathbb{R}^2 satisfaisant à (2) ,or z=u+v est solution,ainsi z= \sqrt[3]{U}+ \sqrt[3]{V} est solution de (1) car on sait que u^3 et v^3 sont solutions de (2) (donc on a u^3=U et v^3=...

Bonsoir. Il me semble que ta solution est correcte mais quand même compliquée .J'ai trouvé beaucoup plus simple ,mais la question que je voulais poser est la suivante: Un polynôme P_n(x)=\sum_{k=0}^n \alpha_k x^k admet il exactement n-solution(s) pour (\alpha_0,\alpha_1,...,\alpha_n)...

Bonsoir. Il me semble que ta solution est correcte mais quand même compliquée .J'ai trouvé beaucoup plus simple ,mais la question que je voulais poser est la suivante: Un polynôme P_n(x)=\sum_{k=1}^n \alpha_k x^k admet il exactement n-solution(s) pour (\alpha_1,\alpha_2,...,\alpha_n)...

Bonsoir à toutes et à tous .:) Soit (1) : x^3+px+q = 0 avec (p,q)\in\mathbb{R}^2 On suppose que z est solution de (1) et que z=u+v et uv=\frac{-p}{3} Montrer que u^3 et v^3 sont solutions de (2): X^2+qX-\frac{p^3}{27} (déjà fait) On pose \Delta le discriminant de (...

Bonsoir à toutes et à tous. On considère l'équation (E) : ax^{3}+bx^{2}+cx+d = 0 où (a;b;c;d) \in\mathbb{R}*\times \mathbb{R}^3 . Montrez que (E) peut se ramener à une équation de la forme : (E'): x^3+px+q = 0 où (p;q) \in \mathbb{R}^2 Je suis sûr qu'il s'...

D'accord, merci de vos réponses . Mais en fait le problème est que je n'arrive pas à rédiger,je ne sais pas si je dois faire une récurrence comme certains me l'avaient dit,ou si je dois faire par double implication...je sais que f(-1)=0 , f(0)=1 et que f n'est pas définie pour x=1 do...

Bonsoir à tous. Il y a une question qui me tracasse,dans un de mes énoncés,j'ai la question suivante : "Montrer qu'on définit une suite de nombres complexes par : u_0=a et u_{n+1}= \frac{1+u_n}{1-u_n} où a est un complexe différent de {-1;0;1} Merci de pouvoir m'aider à répondre à cette questio...

Si tu ne comprends pas ce type de résolution basique par équivalence de proposition,tu vas peut-être galérer pour les équations du \alpha x^{2} + \beta x + \gamma = 0 ... Je suis d'accord pour clore cette discussion qui ,me semble t-il,a été abordée de toutes les manières... A+,cordialement Gauthier.

D'accord,je te remercie de m'avoir rassuré dans la résolution algébrique du calcul,pour l'interprétation géométrique je me pencherai dessus ;-).

Merci à toi Roman.
Bonne soirée à toutes et à tous.

A+,cordialement Gauthier.