Forum de Mathématiques: Maths-Forum

oui à la q-ième . merci encore une fois

x(n)=(0,.....,0,1,0,.......) le 1 à la n ieme place ca marche je crois

voilà ce que j'ai trouvé mais je ne vois pas pourquoi on a l'inégalité dans l'autre sens ni la justification de la première inégalité pour conclure que norme sub est égale à 1
http://img811.imageshack.us/i/numrisation0005k.jpg/

alors 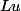est la suite nulle tandis que la norme de vaut .[/quote] . je ne vois pas où est le problème ? on a l'inégalité dans le bon sens

pour montrer cette inégalité j'ai essayé de démontrer que :http://img408.imageshack.us/i/numrisation0004p.jpg/ mais je n'arrive pas

bonsoir , je suis en train de faire un problème de topologie et je bloque sur la question suivante quelqu'un peut m'aider s'i vous plaît . voici l'énoncé :http://img189.imageshack.us/i/numrisation0003mh.jpg/
merci d'avance

ahh oui je vois :lol3: . tu veux montrer qu'aucune sous suite ne peut être de Cauchy et puisqu'on est dans un espace complet on peut conclure . pour la norme sur l^p je choisi quoi comme norme pour faire le calcul je sais qu'elles sont tout équivalente .

oula j'ai oublié de préciser on travaille dans l^p: c' est l'ensemble des suites réelles x=(xi) telles que la serie de terme général (la valeur absolue de xi)^p converge

bonjour , je bloque sur la question suivante : comment je peux démontrer que la suite x(n)= (0,0,....,1,0,....) .[1 à la n eme place 0 partout] n'admet pas de suite extraite qui converge . cordialement

oui je suis d'accord avec toi . mais la construction de la solution en utilisant les endomorphismes ne sera pas la même (je parle de la démarche) .Avec les matrice c'est toujours plus simple puisqu'on manipule facilement les opérations .... merci

J'ai un exo d'algébre linéaire j'arrive à le résoudre avec les matrices ( équivalence des matrices) j'ai essayé de le faire avec les endomorphismes mais j'arrive pas : je crois la methode avec les matrice est la plus simple mais je veux quand meme essayer avec les endomorphismes soit A appartenant à...

j'ai un probléme avec un exercice d'algébre mais ce qui m'intersse c'est pas la solution mais plutôt la démarche pour la construction de la solution construction de la solution Enoncé : Soit E un K espace vectoriel de dimension n .Montrer que si n est pair alors il existe un endomorphisme f de E tel...

en fait on appelle comment ce théorème

:marteau: je le connais pas je vais essayer de la demontrer apres je vais voir en quoi il va nous servir dans mon exo merci

Le fait qu'il existe un et un seul endomorphisme transformant une base donnée à n éléments en un système de n vecteurs :doh: j'ai rien compris mais merci quand meme

Bonjour , je viens de reprendre les cours d'algébgre aprés de longue années de rupture et j'ai perdu pas mal de reflexes . j'aimerai connaitre votre avis sur la solution d'un exercice que je viens de faire Enoncé: E est un espace vectoriel de dimension n . F et G sont deux sous espaces vectoriels de...

soit E un espace vectoriel de dimension n
soit u un endomorphisme de E
alors on a E=Ker(u^n)Im(u^n)
qu'est ce que vous pensez sur ce resultat?

bonjour je ne comprend pas à quoi ça sert de calculer le rang d'un systéme d'équations merci d'avance

bonjour, j'ai une petite question si f et g sont deux endomorphismes de E(espace vectoriel de dimension finie)tel que
fog=gof
alors Imf et kerf sont stables par g
ma question est la suivante est ce que ce resultat est vrai en dimension infinie ,et est ce que la reciproque est vraie merci d'avance

mreci pour tout vos réponses