Ah oui j'ai fait + au lieu de *.
Au temps pour moi.
Encore :
Étudier les variations de la suite géométrique de raison pi / 4 et de premier terme -2.
Là je vois pas la forme, c'est -2 + pi / 4 + pi / 4² ou autre chose ?
16 résultats trouvés
Revenir à la recherche avancée
- 02 Nov 2010, 19:21
- Forum: ✎✎ Lycée
- Sujet: Argument de nombre complexe...
- Réponses: 18
- Vues: 1234
J'ai trouvé :
S = premier terme * (1 - raison^nombre de termes)/(1 - raison)
Mais la raison c'est i ?
Ça ferait 1 * (1 - i^100)/(1 - i) ?
i^100 = 1, non ? Donc 1 - 1 = 0
Donc le résultat serait 1 or, la réponse donnée est 0, où est mon erreur ?
S = premier terme * (1 - raison^nombre de termes)/(1 - raison)
Mais la raison c'est i ?
Ça ferait 1 * (1 - i^100)/(1 - i) ?
i^100 = 1, non ? Donc 1 - 1 = 0
Donc le résultat serait 1 or, la réponse donnée est 0, où est mon erreur ?
- 02 Nov 2010, 18:27
- Forum: ✎✎ Lycée
- Sujet: Argument de nombre complexe...
- Réponses: 18
- Vues: 1234
- 02 Nov 2010, 18:11
- Forum: ✎✎ Lycée
- Sujet: Argument de nombre complexe...
- Réponses: 18
- Vues: 1234
Et j'ai une autre question :
Ecrire le nombre 1 + i + i² + ... + i^99 sous forme algébrique.
Et la réponse est : 0, mais alors là le flou total, quelqu'un peut m'éclaircir ?
Ecrire le nombre 1 + i + i² + ... + i^99 sous forme algébrique.
Et la réponse est : 0, mais alors là le flou total, quelqu'un peut m'éclaircir ?
- 02 Nov 2010, 17:57
- Forum: ✎✎ Lycée
- Sujet: Argument de nombre complexe...
- Réponses: 18
- Vues: 1234
- 02 Nov 2010, 17:56
- Forum: ✎✎ Lycée
- Sujet: Argument de nombre complexe...
- Réponses: 18
- Vues: 1234
Si je factorise par 7, ça me donne :
)
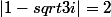
 = \Pi / 3)
Et le 7 en facteur multiplie juste l'argument par 7 ? ?
?
Et sur la correction j'ai -Pi/3, comment on passe de à -Pi/3 ?
à -Pi/3 ?
Et le 7 en facteur multiplie juste l'argument par 7 ?
Et sur la correction j'ai -Pi/3, comment on passe de
- 02 Nov 2010, 17:48
- Forum: ✎✎ Lycée
- Sujet: Argument de nombre complexe...
- Réponses: 18
- Vues: 1234
- 02 Nov 2010, 17:37
- Forum: ✎✎ Lycée
- Sujet: Argument de nombre complexe...
- Réponses: 18
- Vues: 1234
- 02 Nov 2010, 14:41
- Forum: ✎✎ Lycée
- Sujet: Argument de nombre complexe...
- Réponses: 18
- Vues: 1234
- 02 Nov 2010, 10:09
- Forum: ✎✎ Lycée
- Sujet: Argument de nombre complexe...
- Réponses: 18
- Vues: 1234
- 01 Nov 2010, 19:01
- Forum: ✎✎ Lycée
- Sujet: Argument de nombre complexe...
- Réponses: 18
- Vues: 1234
- 01 Nov 2010, 17:43
- Forum: ✎✎ Lycée
- Sujet: Argument de nombre complexe...
- Réponses: 18
- Vues: 1234
Argument de nombre complexe...
Bonjour, j'ai une fiche d'entraînement de calcul mental , où l'on doit donc effectuer des calculs de tête sans poser d'opérations. Un des exemples est le suivant : Calculer l'argument de 7 - 7sqrt{3}i (bon il doit y avoir une erreur d'inatention, c'est un argument et pas l') La réponse donnée est - ...
- 01 Nov 2010, 16:59
- Forum: ✎✎ Lycée
- Sujet: Argument de nombre complexe...
- Réponses: 18
- Vues: 1234
- 14 Mar 2010, 16:08
- Forum: ✎✎ Lycée
- Sujet: Simplifier une division comprenant une racine.
- Réponses: 2
- Vues: 1016
Simplifier une division comprenant une racine.
Bonjour, dans un corrigé d'exercice, notre prof passe de :

à :

J'aimerais savoir comment on fait pour passer de l'une à l'autre.
Merci d'avance.
à :
J'aimerais savoir comment on fait pour passer de l'une à l'autre.
Merci d'avance.
- 14 Mar 2010, 15:48
- Forum: ✎✎ Lycée
- Sujet: Simplifier une division comprenant une racine.
- Réponses: 2
- Vues: 1016
- 30 Déc 2009, 14:19
- Forum: ✎✎ Lycée
- Sujet: Racines et formes factorisée de polynômes
- Réponses: 2
- Vues: 793
Racines et formes factorisée de polynômes
Bonjour, j'ai plusieurs exercices corrigés dont je ne comprend pas la correction. L'énoncé des trois est le même : Trouvez les racines des polynômes donnés et donnez leurs formes factorisées. 1) R(x) = \frac{3}{2}x^2 +5x -1 . 2) S(x) = sqrt{2}x^2 -3x +1 . 3) T(x) = -6x^2 + \f...
- 30 Déc 2009, 13:17
- Forum: ✎✎ Lycée
- Sujet: Racines et formes factorisée de polynômes
- Réponses: 2
- Vues: 793
- 16 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
