Forum de Mathématiques: Maths-Forum

Ben ça peu être aider mais j'arrive toujours pas a déterminer(n) et (n) ...

Bonsoir . J'ai un petit probleme sur un exo : Soit A la matrice : \begin{pmatrix} 1 & 1 & 1 \\ 1 & 0 & 0\\ 1 & 0 & 0 \end{matrix} *Calculer A², A^3 Bon ça va ... *Montrer qu'il existe pour tout n \in \mathbb{N} *, il existe 2 réels \alpha (n) et \beta (n) tels que A^n = \alph...

lut
Pour la 2:
Tu trouve le x pour f(x)=2
Et alors le "x" sera égale à U2 :id:

Ouai c'est pas faux .j'ai carrément zapé le fait que c'était 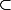et non =
Je viens de comprendre que j'avais rien compris :id:
Bon ba merci de m'avoir aider :we:

J 'ai une question très bête au sujet de la surjectivité. Dans mon cour pour montrer que f est surjective il faut montrer que : Im f =f(E)=F Avec L(E,F) Mais si j'ai bien compris E représente l 'ensemble d'entré et F l'ensemble de sortie Donc on a toujours f(E)=F Pourtant f n'est pas toujours surjec...

ba pas grand chose!
C'était juste pour savoir si y avait un bon site. Sinon c'est pas grave je vais me contenter de mes cours.

bonjour tout le monde.
je ne comprend pas très bien le principe du chapitre des espaces vectoriels même en regardant mes cours.
Connaissez vous des bons sites ou l 'on peut trouver des cour dessus?
Merci d'avance.

pas d'accord?
Pourquoi? :hein:
Mon raisonnement est juste, comme le tien.

réfléchis !!! :marteau:
x -x²
=x(-x)
=x((1- )
:stupid_in (pour thecrash)
-=-

Ce que donne donc =-

:ptdr:

Pour +
Faut factoriser par x.
puis tu factorise par.
Et tu remarque que t'as plus de forme indéterminée :we:

Lut .
utilise la formule d 'Al Kashi et s'est finit
:id:

en fait (910x)'=910

Donc c'est bien 910-130x=130*7-130*x=130(7-x)
compris? :hein:

Non t'as pas juste :!:

130(7-x)=130*(7-x)=130*7-130x=910-130x=...

NB: 130(7-x) n'est pas égale à 130+(7-x)

non j 'ai pas oublié le x!!
(nx)'=n

-130x + 910
910-130x
130*7-130x
...
Fais a*b+a*c=a*(b+c)
... :zen:

f(x) = x*racine(x)-3/16x² ?

Ou sont les parenthèses?
- ?
- ?

écrit comme ça . C'est plus simple a comprendre :id:

Ben t as oublié le "x" lol

Il te reste -130x +910

NB: 910= 130*7 :id:

Donc tu peux factoriser par 130 maintenant?

lut.
Dérive ta fonction !!
Puis tu factorise par 130. :id:
Pour info:
()'=

oups j'avais oublié :briques:

lut.
ben il suffit de résoudre l' équa diff;
f²+2f'+(f')²-m=0
Avec m[- ; 0]

non?