Forum de Mathématiques: Maths-Forum

Ok pas de problème.
Merci quand même.

Thomas

Non non,

Cette preuve est basique.
Je demandais l'explication pour l'exo de Fleur.

Thomas

Oui c'est l'inégalité de Minkowski.

Au fait Chimomo, comment on résout un tel exo : comme je l'ai dit, j'ai jamais vu cette notion de fonction homomorphe.
Ca te dérangerait de faire une preuve rapide ?

Merci

ok merci pour les précisions.
Comment as-tu fait Fleur finalement ?

Thomas

Chimomo, tu utilises l'inégalité triangulaire ?

Sinon, en deux ans de prépa, j'ai jamais vu ce qu'était un holomorphe !

On peut me renseigner ?

Merci

Salut, Effectivement, 3$cos(\frac{1}{z}) ne converge pas quand z tend vers 0 Pour z réel, (on extrapole ensuite aux complexes) Par l'absurde : On suppose que 3$\lim_{z\to 0} cos(\frac{1}{z}) = L (finie) Or, 3$cos(\frac{1}{z})=2cos^2(\frac{1}{2z})-1 Donc 3$\lim_{z\to 0...

Salut,

Encore une autre méthode :



Or, si et sont racines de , alors elles vérifient :



On trouve et et on peut factoriser.

Thomas

Trop tard :++:
confer post 8

J'ai trouvé

Thomas

ah bah encore une journée pour réviser !
N'hésite pas si tu as des questions !!

Thomas

Tu peux donner ta démo aviateurpilot ? :we:

Tu as passé ton concours alors ?

Salut,

Il faut donc qu'un vecteur s'écrive en fonction des deux autres, c'est-à-dire qu'il faut que le déterminant de ces trois vecteurs soir nul.
On trouve que le déterminant vau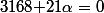t soit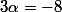

Thomas

salut denver,

Le développement en série entière de cos(x) est :



C'est quoi S^2 ?

Thomas

Pourquoi faire tel ou tel choix ?
C'est surtout une question de feeling...
Tu en essayes un et si ça marche pas alors c'est l'autre.

C'est ok alors ??

C'est une propriété, 3$\forall (a,b) \in \mathbb{R^2} , \fbox{3$(a+b)^n=\sum_{k=0}^n C_n^{k} a^kb^{n-k}=\sum_{k=0}^n a^{n-k} b^k} Or, toi tu veux connaître 3$\sum_{k=0}^n C_n^{k} Cela ressemble donc fortement à 3$(a+b)^n=\sum_{k=0}^n C_n^{k} a^kb^{n-k} sauf qu'il faudrait que...

Pour tout x,

Voilà pourquoi on prend

Thomas

Pour la somme de deux irrationnels, elle peut en effet être un rationnel.

Il suffit de prendre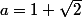 et 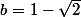qui sont tous deux irrationnels.
Or,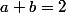 qui est un rationnel.

Thomas

Salut,

Le produit de deux irrationnels est un irrationnel est faux.
On peut prendre le contre exemple suivant :

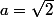et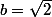
On a donc ab=2 qui est un rationnel

Thomas

En tout cas bonne chance pour ton examen :id: