Forum de Mathématiques: Maths-Forum

Ok, et pour la suite Vn = nr^n? Elle sort d'où?
Et comment trouve-t-on Un= r^n( lambda + nµ) pour un discriminant nul?

ah d'accord, ok j'ai compris. J'ai une autre question: J'ai l'équation caractéristique (qui découle de la relation de récurrence, en posant un= r^n): r² - ar - b = 0. Dans le cas où le discriminant est positif, j'ai 2 racines réelles. (r_1^n)_n et (r_2^n)_n , j'ai \Phi((r_1^n...

Bonjour, J'ai une suite de la forme Un+2 = aUn+1 + bUn. On considère E, l'ensemble des solutions de cette "équation". E est un R-ev, et j'ai: phi: E-> R² (Un)n -> (U0,U1) Je ne comprends pas les démonstrations pour phi surjective, et phiinjective. Pour phisurjective, quelquesoit alpha,beta appartien...

c'est une erreur d'énoncé alors...

merci qd même!

bonsoir,.. je cherche à dériver le champ électrostatique E par rapport à z, mais j'ai pas réussi à trouver le résultat voulu... E= \frac{\lambda.zR}{2.\epsilon_0.(\sqrt{z^2+R^2})^{3/2}} , avec R constant, etc. Et je suis censé trouver: dE/dz= \frac{\lambda.R}{2\epsilon_0}.(\frac{1}{(...

bonjour, j'ai pas très bien saisi la notion de composition de réflexion, de rotation, etc... Comment on peut savoir que c'en est une exactement? Par exemple, j'ai: T'= \begin{pmatrix} 0&1&0\\ -1&0&0\\ 0&0&0 \end{pmatrix} et on me dit que c'est égal à: T'= \begin{pmatrix} 0&am...

bonsoir, je cherche à déterminer la projection de (1,1,0) sur le plan d'équation: x+y=z. donc j'ai le vecteur u(1,1,0), et x, un vecteur appartenant à l'ensemble des vecteurs orthogonaux au plan d'équation x+y=z, de coordonnées (1,1,-1). J'utilise donc p(x) = x - (x|u)/||u||².u mais le x dans l'expr...

Bonjour, j'ai l'application suivante: P(t) -> \int_x^{x+1}P(t)dt , avec P(t)= at²+bt+c (c'est de R² -> F(R,R)). Je souhaite trouver la matrice de cette fonction relativement à la base canonique, mais j'my perds un peu.. J'ai P(t) = [{1/3at^3+1/2bt^3+ct]_x^{x+1} . Comment je fais pour trouver...

Désolé, topic inutile j'ai réussi à trouver la réponse voulue.....

Bonjour, j'ai : a-b-c 0 1 2b -1 0 a+b+c 0 0 si j'utilise le fait qu'on a une matrice triangulaire sup, alors le déterminant est -(a+b+c) par contre, si j'utilise la matrice des mineurs: ca me fait (1)x la matrice: 2b -1 a+b+c 0 donc a+b+c comme déterminant.. où est-ce que j'ai faux? merci

Bonjour,

si j'ai:

t²

le déterminant de cette matrice me donne bien:

t1(1-t²)(-1).t²(1-t²) non? si j'utilise la matrice des mineurs (en utilisant la première colonne)

dans la correction, j'ai:

-t²(1-t²)²....

Oui, je me disais bien.
Mais dans mon cours, on écrit:

(x|y)= x1y1 + x2y2 + x3y3, donc j'ai cru que c'était dû au p.s canonique dans R^n.

Pourquoi ai-je cette expression alors?

Pourriez-vous également m'expliquer pourquoi j'ai les deux expressions ci-dessus pour x et y? merci.

bonjour,

j'ai (x|x)= x1²+x2²+x3² + x1x2+ x1x3 + x2x3.
D'après la déf du produit scalaire sur R^n, j'ai (x|y)= x1y1 + x2y2 + x3y3

je ne comprends pas pourquoi on a :

x= + 1/2(x1y2+x2y1)
y= + 1/2(x1y3 + x3y1) + 1/2(x2y3 + x3y2)

merci

Bonjour,

Je ne comprends pas les égalités (qui proviennent d'une correction d'un exo):

3(j²-j)
= 3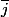-j)
= -3(2iImj)
= -2(2.V3/2)i

Pourquoi:

j²=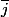

et ce que je ne comprends pas:

= 3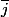-j)
= -3(2iImj)
= -2(2.V3/2)i

merci

Oui, je voulais directement. Ok, ça y est c'est compris, en tout cas merci beaucoup!

Oui non c'est bon en faîte. Et pour la bijectivité?

oui mais ça ne nous dit pas qu'il y en a plusieurs, on pourrait juste conclure que c'est bijectif non?

bonsoir, j'ai beaucoup de mal avec les matrices alors j'aurais plusieurs questions: On me demande si \phi_B était surjective et injective, B étant une matrice. On me propose comme correction: B est inversible. Soit Y une matrice de M2(R) et X= B^-1 Y, alors \phi_B = Y, donc \phi_B est surjective. J'...

y aurais pas une méthode avec un déterminant? j'ai un chiffre qui n'est pas "fini", donc c'est pas très fiable

Bonsoir, Je dois déterminer l'équation d'une tangente passant par un point, en pi/2. J'ai trouvé par quel vecteur il était dirigé (-1/4, -1/2), et par quel point la droite passait: ce point a pour coordonnées (0,1/2) mais voilà, je ne sais pas comment trouver son équation, merci de bien vouloir m'ai...