Forum de Mathématiques: Maths-Forum

romain6929 a écrit:f(a) = epsilon ?

Oui, epsilon = f(a), par exemple. (Attention, c'est à epsilon que l'on donne la valeur f(a), pas l'inverse).
Et on peut faire ce choix car f(a) > 0, car epsilon doit être nécessairement strictement positif.

[quote]comme f est continue en a on a :
quelque soit epsilon>0 il existe n>0 , quelque soit x€R |x-a| |f(x)-f(a)| 0.
Rappel : |f(x)-f(a)| f(a) - epsilon < f(x) < epsilon + f(a)

Peut être n'a-il pas su commencer ... Essaie de le montrer par double inclusion. Pourquoi passer par la double inclusion ? La première idée qui me vient à l'esprit lorsque je vois une différence entre deux ensembles A et B, c'est d'écrire que A-B=A \cap \overline{B} Et c'est en effet un chemin mena...

Voir le produit cartésien comme loi interne m'amenait en effet à penser qu'il avait une certaine somme de propriétés fondamentales et caractéristiques.
La conception de la chose en tant que n-uplets facilite en effet le saisissement.
Merci pour ces lueurs.

2) Si je prends (b,c) avec b dans B et c dans C, il est dans le membre de gauche, mais pas dans le membre de droite ! Une autre manière plus "subtile" d'infirmer la formule : Echange A en B dans le membre de gauche et fait la même chose dans le membre de droite... Merci. Pour ce qui est d...

Bonsoir. Si A et B sont deux parties de E, et C et D deux parties de F, alors on a : 1) (A \times C) \cup (B \times C) = (A \cup B) \times C 2) (A \cup B) \times (C \cup D) = (A \times C) \cup (B \times D) (La propriété 2) m'a été proposée comm...

Une démonstration par l'absurde conviendrait le mieux. Et à un moment donné, il faut procéder par disjonction des cas.

Edit : devancé par Nightmare.
A noter qu'il faut faire référence à la bijectivité de l'application f, sans quoi elle ne serait strictement croissante.

Teacher a écrit:Tu développes avec les formules suivantes:
(a+b)(c+d)= ac+ad+bc+bd
(a+b)²=a²+2ab+b²

Il faut plutôt chercher à factoriser, puisque le but est de transformer cette équation en un produit nul de facteurs du premier degré.

Il ne s'agit pas d'une équation, mais d'une inéquation du second degré.
Pour résoudre celle-ci, tu dois penser à la réécrire sous la forme , puis factoriser le polynôme de gauche.
Tu pourrais alors aisément conclure avec le tableau des signes.

Oui, et c'est une conséquence de la linéarité de la dérivation.

1) Indice :

Puisqu'on s'intéresse à dériver par rapport à x, on considère y comme étant une constante. Du coup, cos(y) est constante, on peut alors écrire a = cos(y) . Il est maintenant possible de considérer la fonction à une seule variable f(x) = a e^x : sa dérivée étant f'(x) = ae...

Bonjour, Voila j'ai eu un cours sur les dérivées partielles, et j'ai loupé la base :doh: Tout simplement... J'ai la fonction f(x,y) = x^2-y^2 je dérive par rapport à x: Ca me donne 2x ok... Maintenant j'ai la fonction f(x,y) = x^2.cos y Je dérive par rapport à x, ça me donne: -2x siny Pourquoi dans...

Qmath a écrit:non pourquoi ?

Parce que si a(k+1) = t, alors a(k) = t + s où s{0,1}
Du coup, a(k+1)-a(k) = t-(t+s) = -s <= 0

Revois les règles des signes !
-(a+b) = - a - b
-(a-b) = - a + b

C'est une simple équation du premier degré.
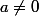
Si tu arrives à l'écrire sous la forme ax + b où x est ton inconnue (et ), l'unique solution serait -b/a.

Intuitivement, la différence devrait être négative..

Pour rappel,
Et

Le minimum de ta fonction est atteint lorsque la dérivée est égale à 0.
La résolution de l'équation f'(x) = 0 te mène donc directement à la solution.

L'expression f(a) avec a=-3/5 n'est sans doute pas correcte, puisque f est définie sur [0,5]