Forum de Mathématiques: Maths-Forum

Merci Ben314 pour ton aide. Je vais donc me renseigner d'avantage sur cette fonction qui semble être la seule solution. Pour JeanJ, il y a des bornes d'intégration (de 0 à l'infini dans les deux cas) ce qui me rajoute des termes dans les ipp (que je n'ai pas écrit) mais qui me permet de les écrire p...

Et la fonction erf c'est la fonction d'erreur c'est bien cela ?
Elle est définit comment ? (je n'avais jamais vu cette fonction jusqu'à hier ^^)

Oui pardon, la deuxième version est faite grâce à un changement de variable de la première. (x=sqrt(x))

Bonjour à tous, Je souhaite intégrer -doublement- la fonction : f(r,z)=\int{\frac{e^{-z/l}e^{-r^2/k}}{\sqrt{r^2+z^2}}}rdrdz (soit vu que l'affichage ne me semble pas clair : [exp^(-z/l)*exp^(-r²/k)]/sqrt(r²+z²)rdrdz et je suis bloqué... Après changement de variable, j'ai réduit cela à f(...

Bonjour à tous, Je voudrais savoir si (de manière similaire à la TF) on a les relations suivantes avec la transformée de Laplace : fonction paire -> fonction impaire après TL fonction impaire -> fonction paire après TL Cela marche pour cos et sin mais j'aurais besoin de généraliser le résultat. Merc...

Bonjour, Merci pour vos réponses, je n'avais pas du tout pensé à utiliser la fonction ln. C'est sûr qu'une fois cette astuce trouvé la suite vient facilement... et on n'est pas d'ailleurs pas obligé d'utiliser la règle de l'hopital (en fait je ne "pouvais" pas l'utiliser ni les DL...) Merci encore e...

C'est ce que j'ai pensé à faire ; mais tout développement fait j'obtiens : (1+tan(t))^{\frac{1}{sin(2t)}}=\Big( {\frac{(1-i)e^{it}+(1+i)e^{-it}}{e^{it}+e^{-it}}\Big) ^{\frac{2i}{e^{2it}-e^{-2it}}}. Et cela ne me lève pas l'indétermination lorsque je fa...

Bonjour à tous,

Voici la limite qu'il me faut résoudre :


Ma calculatrice m'indique mais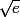 je ne vois pas du tout comment le démontrer.

Merci d'avance de m'aider.

Flipper81