Forum de Mathématiques: Maths-Forum

Messieurs,

Pourquoi mes quelques messages sont effacés ?

Merci pour votre réponse.

Hmm on peut dire que \sin x - x \cos x = \frac{x^3}{3}\Bigprod_{n=0}^{\infty}\left(1-\frac{x^2}{\lambda_n^2}\right) et calculer la dérivée 5ème de ces choses ? Mais j'imagine que l'analyse complexe nécessaire pour faire tout ça n'est pas plus élémentaire que la théorie des résidus. En fait,...

Bonjour à tous, Dans le livre de Thierry Aubin : Differential Geometry, A first Course, il y a un problème (problème 0.44) énoncé comme suit : Suppons que \large\theta_n soient racines positives de l'équation \large tg x = x . Démontrer que \large\sum_{n\geq 1}\frac{1}{\theta_n^2} = \frac{1}{10} Je ...

En général, la réponse est négative.
Par exemple : E = parabole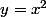 , F = droit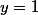
Quand E,F sont bornés, ton impression est vraie car dans ce cas E,F sont compacts. En fait on a : si E est compact, alors E+F est fermé.

Quelles sont les formules de Cauchy ? Il y a un théorème qui permet d'affirmer ça :D. Tu peut lire le théorème 4.17 dans "Lectures on Riemann Surfaces" d'Otto Forster : Suppons que X et Y soient espaces séparés et P: Y\to X un revêtement . Suppons que Z soit simplement connexe, connexe par...

Merci pour votre aide,

Je rajoute la raison pour laquelle j'ai posé la question au-dessus : si on peut démontrer la connexité simple de , on démontrera que toute application holomorphe de dans un tore est constante

Merci pour votre aide.

Oui, le cas est clair, mais le cas où , comment vous le traitez ?

Bjr,

Pourriez-vous m'aider cette question : est-ce que l'espace projectif complexe est simplement connexe ? Et comment le démontrer ?

Merci d'avance