où
649 résultats trouvés
Revenir à la recherche avancée
Re: Demi cercle coupé par 3 cordes.
Je vous propose une solution suivante
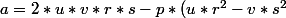<br />\\b=q*(u*r^2-v*s^2)<br />\\c=p*(u*r^2+v*s^2)<br />\\d=q*(u*r^2+v*s^2))
où et
et  sont tels que
sont tels que 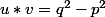 et
et  et
et  sont deux nombres premiers entre eux tels que
sont deux nombres premiers entre eux tels que 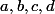 soient positifs.
soient positifs.
où
- 22 Mai 2017, 14:17
- Forum: ⚔ Défis et énigmes
- Sujet: Demi cercle coupé par 3 cordes.
- Réponses: 5
- Vues: 1130
Re: Demi cercle coupé par 3 cordes.
Je vous propose un énoncé plus précis : montrer qu'on peut trouver une infinité de solutions entières au problème des cordes (non proportionnelles entre elles) avec une condition supplémentaire telle que
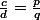 ,
,  et
et  premiers entre eux et
premiers entre eux et 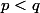 .
.
- 09 Mai 2017, 20:41
- Forum: ⚔ Défis et énigmes
- Sujet: Demi cercle coupé par 3 cordes.
- Réponses: 5
- Vues: 1130
Re: Demi cercle coupé par 3 cordes.
Oui, c'est ça. Je n'avais pas d'image sous la main pour illustrer.
- 02 Mai 2017, 16:40
- Forum: ⚔ Défis et énigmes
- Sujet: Demi cercle coupé par 3 cordes.
- Réponses: 5
- Vues: 1130
Demi cercle coupé par 3 cordes.
Bonjour, J'ai trouvé sur le site ("brilliant.org") le problème de géométrie suivant : étant données les longueurs de 3 cordes consécutives qui coupent un demi cercle, quel est le diamètre ? La relation qui lie les trois longueurs (a,b,c) et le diamètre (d) est la suivante: d^3=d*(a^2+b...
- 29 Avr 2017, 17:40
- Forum: ⚔ Défis et énigmes
- Sujet: Demi cercle coupé par 3 cordes.
- Réponses: 5
- Vues: 1130
Re: Two Galois Group Examples
Oui en effet, c'est pareil que ta solution. Les calculs donnent : (je ne les ai pas faits à la main, voir le code Magma plus bas...) [Edit: j'ai rajouté l'application numérique] N=p^3 + 2q^3 + 4r^3- 6pqr P(j\alpha)P(j^2\alpha)= p^2 - 2qr+(2r^2- pq)\alpha + (q^2-pr) \a...
- 14 Déc 2016, 15:39
- Forum: ✯✎ Supérieur
- Sujet: Two Galois Group Examples
- Réponses: 31
- Vues: 1624
Re: Two Galois Group Examples
Désolé, en effet pour qu'il y ait un petit intérêt à ma formule, il faut expliciter le passage de \mathbb{Q}[\alpha] à \mathbb{Q}[x]/(x^3-2) . A p+r*\alpha+q+\alpha^2 on fait correspondre P(x)=p+r*x+q*x^2 soit j solution de x^2+x+1 , les trois racines de x^3-2 sont \alpha , j*\alpha ...
- 13 Déc 2016, 21:48
- Forum: ✯✎ Supérieur
- Sujet: Two Galois Group Examples
- Réponses: 31
- Vues: 1624
Re: Two Galois Group Examples
Oups, c'était juste pour apporter une (petite) contribution. J'ai mis un point d'interrogation, mais juste rhétorique... Je me suis posé la question d'une formule pour l'inverse, n'utilisant pas l'algèbre linéaire. Du coup, notons a,b,c les trois racines (de \matbb{C} \setminus \mathbb{Q } ) de X^3 ...
- 12 Déc 2016, 18:28
- Forum: ✯✎ Supérieur
- Sujet: Two Galois Group Examples
- Réponses: 31
- Vues: 1624
Re: Two Galois Group Examples
Peut-être que le plus simple ici est d'identifier cet ensemble à Q[X]/(X^3-2), et de montrer que X^3-2 est irréductible sur Q ?
- 11 Déc 2016, 22:50
- Forum: ✯✎ Supérieur
- Sujet: Two Galois Group Examples
- Réponses: 31
- Vues: 1624
Re: Equivalent d'une suite recurrente
Bonsoir ! Même genre que celle-ci : http://www.ilemaths.net/sujet-developpement-limite-d-une-fonction-dependant-d-un-parametre-719625.html Oui, tout est dans le log et un "télescopage": \ln(u_{n}) = 2^n\big( \ln(u_0) + \sum_{i=0}^{n-1}\frac{1}{2^{i+1}}\ln(1+\frac{1...
- 22 Nov 2016, 16:39
- Forum: ✯✎ Supérieur
- Sujet: Equivalent d'une suite recurrente
- Réponses: 6
- Vues: 864
Re: formules pour ses calculs?
En effet, fais un petit effort
http://lmgtfy.com/?q=cours+statistique+probabilit%C3%A9+informatique
http://lmgtfy.com/?q=cours+statistique+probabilit%C3%A9+informatique
- 20 Mar 2016, 10:31
- Forum: ✯✎ Supérieur
- Sujet: formules pour ses calculs?
- Réponses: 3
- Vues: 351
Re: Problème de théorie des nombres
Oui, pour résumer, on a donc: Soit a un élément d'un corps fini \mathbb{K} . Si x^2-a et x^2+a sont irréductibles dans \mathbb{K} , alors pour tout entier n\ge 2 , x^{2^n}-a et x^{2^n}+a sont aussi irréductibles dans \mathbb{K} . Ce résultat me sert d'illustration dans un papier sur les isomorphisme...
- 16 Mar 2016, 09:42
- Forum: ⚜ Salon Mathématique
- Sujet: Problème de théorie des nombres
- Réponses: 7
- Vues: 796
Re: Problème de théorie des nombres
Bon, je pense que c'était la bonne approche : Soit a un élément de \mathbb{F}_p à p éléments, soit \alpha une racine de a dans \mathbb{F}_{p^2} L'autre racine de a est \alpha^p (car conjuguée) donc \alpha^{p-1}=-1 . Les deux racines de -a sont donc \alpha^{(p+1)/2} et \alpha^{(3p-1)/...
- 15 Mar 2016, 17:08
- Forum: ⚜ Salon Mathématique
- Sujet: Problème de théorie des nombres
- Réponses: 7
- Vues: 796
Re: Problème de théorie des nombres
Je pense que le cas de 2 n'est pas particulier pour la suite. Il faudrait que je puisse juste obtenir pour l'induction ceci: Si a et -a ne sont pas des carrés dans un corps fini \mathbb{F} , alors leurs racines carrées dans une extension quadratique, \mathbb{F}[x]/(x^2-a) par exemple, ne son...
- 15 Mar 2016, 16:23
- Forum: ⚜ Salon Mathématique
- Sujet: Problème de théorie des nombres
- Réponses: 7
- Vues: 796
Re: Problème de théorie des nombres
Merci, bien vu! Cela me donne la réponse à la première partie. Pour la deuxième, je vais tenter une récurrence... A suivre!
- 14 Mar 2016, 14:24
- Forum: ⚜ Salon Mathématique
- Sujet: Problème de théorie des nombres
- Réponses: 7
- Vues: 796
Problème de théorie des nombres
Bonjour, Au cours d'une recherche, je tombe sur la propriété suivante qui semble vraie expérimentalement mais dont je n'ai pas encore de démonstration: soit p un nombre premier congru à 5 modulo 8, alors 2 et -2 n'ont pas de racine carrée dans \mathbb{F}_p (corps à p éléments) et même plus : pour to...
- 14 Mar 2016, 12:40
- Forum: ⚜ Salon Mathématique
- Sujet: Problème de théorie des nombres
- Réponses: 7
- Vues: 796
On peut quand même essayer de se faire une idée "constructive" d'une fonction non continue sans l'axiome du choix.
En se restreignant par exemple aux seuls réels de la forme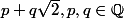 et en définissant
et en définissant  = q) par exemple.
par exemple.
En se restreignant par exemple aux seuls réels de la forme
- 28 Avr 2015, 16:53
- Forum: ✯✎ Supérieur
- Sujet: Construction du log
- Réponses: 19
- Vues: 1325
muse a écrit:Sauf qu'on a dit que si la fonction était continue en un point alors elle l'était partout. Par conséquent tes fonctions sont discontinues en tout point alors ?
ben oui forcément.
- 27 Avr 2015, 21:27
- Forum: ✯✎ Supérieur
- Sujet: Construction du log
- Réponses: 19
- Vues: 1325
Par curiosité, je me suis demandé quelles étaient les solutions non continues.
Une réponse (existentielle, non constructive) est donnée par les bases de Hamel et la solution à l'équation fonctionnelle de Cauchy
Georg Hamel
équation fonctionnelle de Cauchy
Une réponse (existentielle, non constructive) est donnée par les bases de Hamel et la solution à l'équation fonctionnelle de Cauchy
Georg Hamel
équation fonctionnelle de Cauchy
- 27 Avr 2015, 15:07
- Forum: ✯✎ Supérieur
- Sujet: Construction du log
- Réponses: 19
- Vues: 1325
allmess a écrit:Merci
Alors (f²-f)²=f;)-2f³+f>=0 (signe constant donc..)
Avec
Et donc (f²-f)=0 D'où le résultat..?
oui si tu as une condition supplémentaire de continuité
- 22 Avr 2015, 06:31
- Forum: ✯✎ Supérieur
- Sujet: Égalité entre integrales
- Réponses: 5
- Vues: 994
- 21 Avr 2015, 20:12
- Forum: ✯✎ Supérieur
- Sujet: Égalité entre integrales
- Réponses: 5
- Vues: 994
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
