31 résultats trouvés
Revenir à la recherche avancée
- 02 Nov 2009, 21:58
- Forum: ✎✎ Lycée
- Sujet: Tableau de variations
- Réponses: 4
- Vues: 692
Ces limites que je dois calculer en 1- et 1+ complètent le tableau de variations c'est bien ça ?
Et sinon je dois calculer le point d'intersection A de la courbe f avec l'axe des abscisses. Comment faire ?
Et sinon je dois calculer le point d'intersection A de la courbe f avec l'axe des abscisses. Comment faire ?
- 02 Nov 2009, 20:08
- Forum: ✎✎ Lycée
- Sujet: Tableau de variations
- Réponses: 4
- Vues: 692
Tableau de variations
Bonjour, j'aurais besoin d'un petit coup de main svp. Je dois chercher la dérivée de \frac{2x+3}{x-1} J'ai trouvé \frac{-5}{(x-1)^2} : Est-ce juste ? Ensuite, je dois faire le tableau de variations : f'(x)=0 \Delta =0 Une seule solution : x=1 ( car \frac{-b}{2a} =1 ) f(x) sera décroissante p...
- 02 Nov 2009, 12:23
- Forum: ✎✎ Lycée
- Sujet: Tableau de variations
- Réponses: 4
- Vues: 692
- 01 Nov 2009, 20:58
- Forum: ✎✎ Lycée
- Sujet: Fonction dérivée
- Réponses: 3
- Vues: 363
La dérivée sera tout le temps de signe négatif puisque numérateur < 0 et dénominateur > 0 .
Mais est-ce que mon raisonnement pour le tableau de variations est juste ?
Mais est-ce que mon raisonnement pour le tableau de variations est juste ?
- 01 Nov 2009, 20:10
- Forum: ✎✎ Lycée
- Sujet: Fonction dérivée
- Réponses: 3
- Vues: 363
Fonction dérivée
Bonjour, j'aurais besoin d'un petit coup de main svp. Je dois chercher la dérivée de \frac{2x+3}{x-1} J'ai trouvé \frac{-5}{(x-1)^2} : Est-ce juste ? Ensuite, je dois faire le tableau de variations : f'(x)=0 \Delta =0 Une seule solution : x=1 f(x) sera décroissante pour tout x dans mon table...
- 01 Nov 2009, 19:58
- Forum: ✎✎ Lycée
- Sujet: Fonction dérivée
- Réponses: 3
- Vues: 363
C'est bien pour cela que la question a) apparait devant toi.
Si [RS] = 10 ; M appartient à [RS] ; RM = x
Alors x = un nombre compris entre 0 et 10
0 et 10 ne sont pas pris en compte bien sûr.
Si [RS] = 10 ; M appartient à [RS] ; RM = x
Alors x = un nombre compris entre 0 et 10
0 et 10 ne sont pas pris en compte bien sûr.
- 07 Oct 2009, 14:54
- Forum: ✎ Collège et Primaire
- Sujet: 3émé dm
- Réponses: 9
- Vues: 761
- 07 Oct 2009, 14:48
- Forum: ✎✎ Lycée
- Sujet: Equation à résoudre
- Réponses: 3
- Vues: 381
Bonjour, tu as là un exercice sur le théorème de Thalès.
Si je me base sur ton énoncé :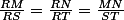
a) M appartient à [RS]
[RS] = 10cm
Conclusion ?
Si je me base sur ton énoncé :
a) M appartient à [RS]
[RS] = 10cm
Conclusion ?
- 07 Oct 2009, 14:41
- Forum: ✎ Collège et Primaire
- Sujet: 3émé dm
- Réponses: 9
- Vues: 761
Equation à résoudre
Bonjour à tous, quelqu'un peut m'aider à résoudre cette équation svp car je bloque ? Comme cela mon système sera résolu. Merci d'avance.
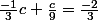
- 07 Oct 2009, 14:30
- Forum: ✎✎ Lycée
- Sujet: Equation à résoudre
- Réponses: 3
- Vues: 381
Inconnues
Bonjour à tous, j'ai de nouveau un souci car nouveau dm de maths. J'ai fait tout les exos demandés sauf un car je bloque aux 2 dernières questions : lim g(x) = +oo quand x tend vers 0 lim g(x) = 1 quand x tend vers +oo Si x=1 ou x=3 ; g(x)=0 Asymptotes verticale ( x=0 ) et horizontale ( y=1 ) présen...
Salut !
16y = -24x + 48
y = -24x/16 + 48/16
y = -1,5x + 3
Voilà normalement ce que tu trouve en ne changeant pas le signe.
Maintenant, si tu veux trouver x, reprend l'équation de départ et remplace y par la "fonction affine" trouvée et résoud ;)
16y = -24x + 48
y = -24x/16 + 48/16
y = -1,5x + 3
Voilà normalement ce que tu trouve en ne changeant pas le signe.
Maintenant, si tu veux trouver x, reprend l'équation de départ et remplace y par la "fonction affine" trouvée et résoud ;)
- 04 Oct 2009, 08:29
- Forum: ✎✎ Lycée
- Sujet: Petite précision
- Réponses: 5
- Vues: 655
Heu je ne pense pas être d'accord car Fox vient de me dire que la fonction est :
(x/1) + x
Or toi Ericovitchi, tu a utilisé celle-ci : x / (1+x)
Ce que j'ai mis en rouge est la partie indépendante de la fraction.
A moins que Fox se soit trompé en me la dictant.
(x/1) + x
Or toi Ericovitchi, tu a utilisé celle-ci : x / (1+x)
Ce que j'ai mis en rouge est la partie indépendante de la fraction.
A moins que Fox se soit trompé en me la dictant.
- 04 Oct 2009, 08:20
- Forum: ✎✎ Lycée
- Sujet: Exercice Dérivées
- Réponses: 15
- Vues: 1825
Ok donc pour ma part ton raisonnement du post de 19h01 est faux Ce 1 appartient à la fraction, on ne peut donc pas le déplacer de l'autre côté tout seul. Soit c'est la fraction, soit c'est rien du tout. Et puis : x/1 = x divisé par 1 = x f(x) = x/1 + x < 1/11 f(x) = x + x < 1/11 Il me semble.. Je te...
- 03 Oct 2009, 20:09
- Forum: ✎✎ Lycée
- Sujet: Exercice Dérivées
- Réponses: 15
- Vues: 1825
- 31 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
