Forum de Mathématiques: Maths-Forum

Bonsoir, dernières révisions avant l'épreuve de demain, j'ai décidé de faire queqlues exos dont des exos de probas, ceux tombés au bac d'Asie et de Guyane/Antilles. Mon problème est le suivant : je n'arrive pas à calculer des probabilités ... Suivant les exercices, les formules changent tout le temp...

D'accord, merci :)

J'ai vu dans mon livre que pour calculer je peux utiliser ma calculatrice et faire comme si je calculais . Cette méthode me donne la bonne réponse. Cependant, est-elle valable dans une copie au Bac ?

Euh.. Je ne suis pas sur d'avoir compris la :/

Il y a quelque chose que je ne comprends pas très bien Dans la partie D de l'exercice 1, pourquoi P(D<880)=0.5+P(800 ;) D ;) 880) ? Je ne comprends pas d'ou viennent 800 et 880. Voici l'énoncé http://www.ti-bank.fr/modules/archives/downloads/Maths_TS_CE_2013.pdf et un corrigé : http://www.cours-sowa...

C'est parfait, merci à vous deux ! :)

Merci ! :)

Par exemple, je sais calculer dans une lois normale de paramètre 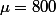et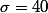
Comment fait-on pour calculer les 2 autres probabilités que j'ai énoncé au dessus ?

Oui oui ça j'en suis conscient !

Bonjour, A quelques jours du bac, j'aimerai que vous m'aidiez à faire le point sur les différentes formules pour calculer des probabilités avec la loi normal de paramètre [\mu;\sigma] On va désigner ici par "x" la probabilité à calculer Comment calculer P(a \leq X \leq b) ? Comment...

Problème résolu, la solution est bien

Merci

Bonjour, Non ce n'est pas avec le plus devant la racine carrée, ça donne un nombre réel mais négatif. Pour x=\frac{5+\sqrt{29}}{2} A la calculatrice je trouve : 6-\frac{5}{\frac{5+\sqrt{29}}{2}+1} Et ça me donne environ 5.42 alors que \frac{\sqrt{29}+5}{2}=5.2 J'avoue que ça me laisse sans voix ...

Haaaaaa mais oui !! Oui oui je sais comment obtenir la meme égalité que toi, c'est juste que ce qui me genait était que delta étant positif, il y a donc deux solutions à mon équation sauf que la consigne dit bien que cette équation est à résoudre dans R+ Je trouve donc x=\frac{-5-\sqrt{29}}{-2} Mais...

Je viens de le refaire vite fait et on trouve ensuite
D'ou ?

oui j'avais déjà essayé de faire comme ça mais après j'étais bloqué car on obtient un polynome du second degrés et son discriminant n'étant pas nul, il y a deux solutions et l'énoncé ne parle que d'une seule solution

Oui je sais, j'ai bien compris l'énoncé mais je n'arrive pas à le faire :(

Bonsoir (ou re-bonsoir) J'ai une petite question sur un exercice Comme dis dans le titre, dans un exercice je dois résoudre l'équation f(x)=x Voici l'énoncé de l'exercice Soit f, la fonction défini sur [0;+\infty[ par f(x)=6-\frac{5}{x+1} On considère la suite u_n définie par u_0 =0 et pour ...

Merci de ton aide ! Je suis content d'avoir réussi à résoudre ça ! :)

Ha d'accord ! Donc pour la première question c'est bon, merci ! Pour la deuxième je trouve bien la réponse demandée mais je ne suis pas sur de mon raisonnement ! \frac{4e^{nx}}{e^{nx}+7} 4e^{nx}=2e^{nx}+14 2e^{nx}=14 e^{nx}=\frac{14}{2} ln(e^{nx})=ln(7) nx=ln(7) x=\frac{ln...

Bonsoir, Je viens ici ce soir car j'ai quelques petits sourcis dans la résolutions d'un exercice portant sur l'étude d'une fonction qui est : f_n(x)=\frac{4e^{nx}}{e^{nx}+7} 1) Démontrer que pour tout entier naturel n, non nul, le point A(0,0.5) appartient à C_n J'ai simplifié par e^{nx} le ...