Forum de Mathématiques: Maths-Forum

selon les valeurs de k on calcule la somme on a 2 cas si n divise r (dans le cas de n=1) alors c'est 1 si n ne divise pas r alors c'est o c'est ma faute j'ai parlé just du cas general pour qustion 2 pour tt n de N* on pose n-1 ;) ((Zn)^ k²) = Gn k=0 a-montrer que pour j de N on a n-1 ;) ((Zn)^ (k+j)...

slt j'ai besoin d'aide dans cet exercice pour n de N* fixé. on pose Zn=exp(2i/n) 1-calculer selon r de Z la valeur de n-1 ;) (Zn)puissance kr ""le resultat c 0"" k=0 2- pour tt n de N* on pose n-1 Gn= ;) (Zn)puissance k² k=0 a-montrer que pour j de N on a n-1 Gn= ;) (Zn)puissance (k+j)² k=0 on poura...

desole c
(1+2+..........+n)puissance 2=1³+2³+.....+n³
je vois pas pourquoi c'est pose dans l'exercice il ne sert je crois a rien
pour l'argument c'est tres convainquant il me reste de le bien rediger merci beaucoup

bonjour



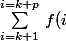comme les f(i) sont tous distincts et supérieurs ou égaux à 1,
a minima, la somme est nécessairement supérieure ou égale à 1+2+..+p.

tt a fait logique mais comment le demontrer ?


merci pour les reponses

bonjour tt le monde voila un exercice qui me casse la tete soit f une bijection de N* dans N* Sn= ;) f(k)/k² de k=1 jusqu'a n 1- on montre que (1+2+..........+n)=1³+2³+.....+n³ c facil par recurrence 2- montrer que pour tout n de N* on a 2n ;) f(k) ;) n(n+1)/2 k=n+1 j'ai essaye par recurence mais 2n...