24 résultats trouvés
Revenir à la recherche avancée
Pour la question préliminaire, j'ai trouvé que la hauteur valait h=a.\frac{sqrt{3}}{4} (grâce au théorème de Pythagore) ce qui fait bien A_{ABC}=\frac{B.h}{2}=\frac{a.a.\frac{sqrt{3}}{4}}{2}=a^2.\frac{sqrt{3}}{4} Car B=a . 1. A l'étape 0 il y a 3 côtés (je ne sais pas s'il faut garder a ou choisir 1...
- 28 Nov 2010, 13:19
- Forum: ✎✎ Lycée
- Sujet: aire d'un triangle équilatéral, suites
- Réponses: 5
- Vues: 1185
Alors oui,  correspond au nombre de côtés à l'étape n et
correspond au nombre de côtés à l'étape n et 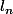 correspond à la longueur d'un côté à l'étape n
correspond à la longueur d'un côté à l'étape n
- 27 Nov 2010, 16:53
- Forum: ✎✎ Lycée
- Sujet: aire d'un triangle équilatéral, suites
- Réponses: 5
- Vues: 1185
aire d'un triangle équilatéral, suites
Bonjour tout le monde, je m'adresse à vous car un devoir maison me pose quelques difficultés. L'exercice se base sur le principe des flocons de von koch. Voici l'énonce : c_n correspond au nolbre de côtés à l'étape n et l_n correspond à la longueur d'un côté à l'étape n Préliminaire : Démontrer que...
- 27 Nov 2010, 16:26
- Forum: ✎✎ Lycée
- Sujet: aire d'un triangle équilatéral, suites
- Réponses: 5
- Vues: 1185
Je ne comprend pas vraiment... Tu m'as rappelé que '=2e^{2x}) , donc
, donc  .
.
Et la dérivée de g(x), g'(x)=1-0+4+1=6 ( la 1 correspond à la dérivée de x, le 4 à la dérivée de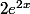 et le 1 à la dérivée de
et le 1 à la dérivée de 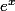
Et la dérivée de g(x), g'(x)=1-0+4+1=6 ( la 1 correspond à la dérivée de x, le 4 à la dérivée de
- 17 Oct 2010, 13:28
- Forum: ✎✎ Lycée
- Sujet: Exercice sur une fonction exponentielle
- Réponses: 6
- Vues: 1089
- 17 Oct 2010, 12:57
- Forum: ✎✎ Lycée
- Sujet: Exercice sur une fonction exponentielle
- Réponses: 6
- Vues: 1089
- 17 Oct 2010, 12:29
- Forum: ✎✎ Lycée
- Sujet: Exercice sur une fonction exponentielle
- Réponses: 6
- Vues: 1089
Exercice sur une fonction exponentielle
Bonjour tout le monde ! J'ai un exercice qui me pose quelques difficultés, particulièrement pour la 2e partie. L'exercice est le suivant : 1) Soit g la fonction définie sur \mathbb{R} par g(x)=x-2+ e^{2x}+e^{x} a- Etudier les variations de g sur \mathbb{R} g'(x)=1+e^{2x}+e^{x}\gt 0 car e...
- 17 Oct 2010, 11:17
- Forum: ✎✎ Lycée
- Sujet: Exercice sur une fonction exponentielle
- Réponses: 6
- Vues: 1089
Exercice sur les nombres complexes
Bonsoir à tous ! J'ai un exercice qui me pose quelques soucis car il ne faut pas se tromper dans le calcul, l'exercice est la suivant : On pose z=x+iy où x et y sont deux nombres réels et Z=\frac{z+i }{z-i } . 1°) Déterminer Re(z) et Im(z) en fonction de x et y Z = \frac{z+i}{z-i} = \frac{(x+iy&...
- 25 Sep 2010, 20:00
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les nombres complexes
- Réponses: 1
- Vues: 588
- 12 Sep 2010, 18:08
- Forum: ✎✎ Lycée
- Sujet: Un problème de calcul d'aire
- Réponses: 1
- Vues: 606
Un problème de calcul d'aire
Bonjour à tous, un exercice me pose quelques difficultés, disons plutot une question : Soit H l'hyperbole d'equation y= \frac{1}{x} representée dans le repère orthonormal ci-dessus. Soit h un réel positif. Les points de la figure sont définis ainsi : - B(1;0) et C(1+h;0) - BCDE et BCGF sont des rect...
- 12 Sep 2010, 15:48
- Forum: ✎✎ Lycée
- Sujet: Un problème de calcul d'aire
- Réponses: 1
- Vues: 606
Quelques aires à calculer
Bonjour à tous ! :). Il s'agit d'un devoir qui me pose quelques petites difficultés : Soit H l'hyperbole d'equation y= 1/x representée dans le repère orthonormal ci-dessus. Soit h un réel positif. Les poitns de la figure sont définis ainsi : - B(1;0) et C(1+h;0) -BCDE et BCGF sont des rectangles - E...
- 11 Sep 2010, 16:27
- Forum: ✎✎ Lycée
- Sujet: Quelques aires à calculer
- Réponses: 0
- Vues: 614
- 05 Sep 2010, 20:22
- Forum: ✎✎ Lycée
- Sujet: Petite fonction
- Réponses: 10
- Vues: 1104
Je cherche.. mais je ne trouve pas comment vous trouvez cette dérivée. La fonction n'est pas de la forme u/v ?!
- 05 Sep 2010, 19:05
- Forum: ✎✎ Lycée
- Sujet: Petite fonction
- Réponses: 10
- Vues: 1104
Merci pour ta réponse :).
En dérivant j'ai trouvé : f'(x)= 2x²-8x/(x-2)²
Mais je suis pas sur que ce soit bon car lorsque je continue, quand j'étudie le signe de la dérivée, je trouve 4 et 0 en valeur interdite..
En dérivant j'ai trouvé : f'(x)= 2x²-8x/(x-2)²
Mais je suis pas sur que ce soit bon car lorsque je continue, quand j'étudie le signe de la dérivée, je trouve 4 et 0 en valeur interdite..
- 05 Sep 2010, 16:52
- Forum: ✎✎ Lycée
- Sujet: Petite fonction
- Réponses: 10
- Vues: 1104
Je suis en première. Et je sais faire un tableau de variation, il faut d'abord que je dérive la fonction... ?
- 05 Sep 2010, 16:11
- Forum: ✎✎ Lycée
- Sujet: Petite fonction
- Réponses: 10
- Vues: 1104
Petite fonction
Bonsoir, J'aurais besoin de votre aide pour un exercice tout simple .. mais je ne sais plus comment daire :(. Soit la fonction f définir sur ]2;+infinir[ par f(x)=2x²/x-2 => Quelle est la plus petite valeur prise par f(x) lorsque x varie de 3 à 5 ?! Et la plus grande ?! Merci d'avance pour votre aid...
- 04 Sep 2010, 22:18
- Forum: ✎✎ Lycée
- Sujet: Petite fonction
- Réponses: 10
- Vues: 1104
Suite
Est ce que je suis sur la bonne voie ?!
- 01 Mar 2010, 19:41
- Forum: ✎✎ Lycée
- Sujet: Charpente et Barycentre
- Réponses: 3
- Vues: 669
Réponse
Je me suis trompée de question, celle que j'ai écrit a seulement été une question que je me suis posée. La question 1 était en fait : Quel point retrouve-t-on pour n=2 et p=3 ? Et pour n=3 et p=4 ? Pour la question 2, les poids affectés à Gn,p correspondent à tous les poids affectés à P, Q, R et S r...
- 28 Fév 2010, 20:34
- Forum: ✎✎ Lycée
- Sujet: Charpente et Barycentre
- Réponses: 3
- Vues: 669
Charpente et Barycentre
Bonjour tout le monde, j'ai presque fini mon devoir maison de mathématiques, il ne me reste qu'une question qui généralise en fait la question précédente. A, B, C et D représentent quatre coins non coplanaires du toit d'un bâtiment moderne sur lequel on veut construire une charpente. On utilise cin...
- 28 Fév 2010, 17:10
- Forum: ✎✎ Lycée
- Sujet: Charpente et Barycentre
- Réponses: 3
- Vues: 669
Merci beaucoup pour ton aide :happy2: .
Cependant pour la dernière question, j'ai trouvé en associant les pondérations de P, Q, R et S à celles de G, que G était le barycentre de (R;6),(Q;4),(P;4),(S,6).
Et je ne sais pas si c'est correct et si ça l'ai, si ça réponds à ma question.
Cependant pour la dernière question, j'ai trouvé en associant les pondérations de P, Q, R et S à celles de G, que G était le barycentre de (R;6),(Q;4),(P;4),(S,6).
Et je ne sais pas si c'est correct et si ça l'ai, si ça réponds à ma question.
- 14 Fév 2010, 12:42
- Forum: ✎✎ Lycée
- Sujet: Charpente et Barycentre
- Réponses: 6
- Vues: 867
- 24 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
