Forum de Mathématiques: Maths-Forum

Nightmare a écrit:Salut,

B(t)=(0,0,0) ? :lol3:

B doit être non nul

Bien le bonjour, j'aimerai avoir connaissance du théorème de Sylvester et sa preuve (Matriciellement).
Merci

Bien le bonjour à vous,
Je travaille sur les systèmes différentiels et j'ai un problème.

J'aimerai trouver un vecteur B(t)=(a(t), b(t), c(t)) de tel que .

Merci d'avance

J'ajoute que <, > est le produit scalaire associé à la norme euclidienne

Bien le bonjour à vous, j'ai une préocupation par raport à une proposition j'aimerai la démontrer: la voici: Pour qu'une équation différentielle A(x)y''+2B(x)y'+C(x)y=0 (où A(x), B(x) et C(x) sont des polynômes) admette une solution polynomiale, il est nécessaire ...

Bien le bonjour à vous j'ai un problème avec une égalité j'aimerai savoir comment on l'a.La voici: f(a+x)-f(x)== où K est une application de classe C^1 d'un espace vectoriel de dimension fini E vers M_n(IR) , f une fonction numérique sur E, A la matrice hessienne de f en a et...

Bonjour. La prise d'adjoint est (anti)linéaire, elle commute donc avec la dérivation. (dérivation des fonctions composées, en se souvenant que la différentielle d'une application (anti)linéaire en un point est l'application elle-même) merci beaucoup mais je ne comprends pas très bien j'aimerai que ...

J'aimerai comprendre une égalité sur les adjoints.
Soit r(t) et r(t)* son adjoint j'aimerais savoir pourquoi .
Merci d'avance

J'aimerai comprendre une égalité sur les adjoints.
Soit r(t) et r(t)* son adjoint j'aimerais savoir pourquoi .
Merci d'avance

Bien le bonjour à vous. Je travail pour un mémoire et je voudrais comprendre une égalité.
La voici
.
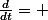
J'aimerai donc savoir comment a lieu cette égalité
Merci d'avance

Bien le bonjour à vous.
Dans le cadre de mes travaux j'ai eu une difficulté. J'aimerai justifier l'égalité suivante

où A est une application linéaire (matrice), K une application linéaire (matrice et le produit scalaire sur IR

Merci d'avance

Merci a tous pour vos aides,j'ai trouvé satisfaction à mon problème

je crois que vous n'avez pas bien saisi mon pb.
J'ai f une fonction définie sur un espace de Banach, et sa différentielle seconde, je veux montrer que est bilinéaire symétrique.

Merci d'avance

Bien le bonjour à vous,
J'aimerai savoir comment faire pour montrer que la différentielle seconde d'une application est une application bilinéaire symétrique

Merci d'avance

Bien le bonjour à vous, j'ai un pb avec la démo d'un théorème, Voici le théorème: Soit E, F et G trois espaces vectoriels normés de dimensions finies. Soit f une application de E vers F et g une application de F vers G. Si f et g sont de classe C^{k} , alors fog est de classe C^{k} Merci d'avance

sin;) + icos;) = e^???????? en faite je voudrai la forme exponentielle e^(?????) Merci Ton problème est simple, en fait il suffit de remarquer que sin\alpha=cos(\frac{\pi}{2}-\alpha) et que cos\alpha=sin(\frac{\pi}{2}-\alpha) tu obtiendra donc sin;) + icos;)= e^{(\frac{\pi}{2}-\...

Bien le bonjour à vous, j'aimerai avoir votre aide par rapport à un problème que je rencontre ces derniers temps. Voici le problème : Dans l'anneau Z[i] on considère les deux éléments u=11+7i et v=3+7i. 1. déterminer le pgcd(u,v) 2. En déduire une combinaison linéaire des éléments de Z[i] Merci d'av...

girdav a écrit:Bonjour.
devrait t'aider.

Bonjour
ta formule a une petite éreur c'est plutôt

Salut, Tu dois utiliser les séries entières pour résoudre ton problème. En effet tu doit poser y=\sum_{i=1}^n a_{i}x^i ensuite tu dérives deux fois y. Puis tu calcule la première partie de ton équation différentielle et enfin tu trouvera les conditions sur les coefficients a_{i} pour que y soit solu...

Et bien soit tu utilises une formule de dérivation pour ce genre de fonctions à valeurs vectorielles, soit tu la calcules à la main: \phi(t)=\sum_{i}(b-a)_if_i(a+t(b-a)) et donc tu dois avoir: \phi^{'}(t)=\sum_{i}(b-a)_i\frac{d(f_i(a+t(...