Forum de Mathématiques: Maths-Forum

Personne ?

Je crois qu'on peut faire un peu mieux que ça en réalité. Donnons-nous une mesure positive mu et une fonction f mu-mesurable. On commence déjà par définir l'intégrale des fonctions simples. Ensuite, par limite, on définit l'intégrale des fonctions positives. A ce stade là, on autorise les fonctions ...

Salut tout le monde, Il semblerait que le résultat suivant soit vrai: \forall (u_n) \subset W^{1,p}(\Omega) \quad \forall u \in W^{1,p}(\Omega) \quad u_n \rightharpoonup u \quad \text{dans $W^{1,p}(\Omega)$} \quad \Leftrightarrow \quad \Bigg( u_n \rightharpoonup u...

Je suis désolé. Je pensais que c'était clair.

X est une variable aléatoire. A priori, il n'y a pas d'hypothèse dessus.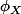 est la fonction caractéristique de X.

Salut tout le monde,

Je suis tombé sur une inégalité que je n'arrive pas à expliquer dans une preuve de proba.
La voilà:



Est-ce que vous avez une idée d'où peut bien venir ce résultat ?

mrif a écrit:Qu'est-ce que tu as comme définition de la connexité?

J'ai la définition qui dit qu'un connexe ne peut pas être l'union de deux de ses ouverts non vides et disjoints.

Bonjour,

J'ai du mal à voir pourquoi un intervalle est connexe. Est-ce que vous pourriez m'expliquer cela en utilisant aucun prérequis ?

Merci par avance.
Boris.

Le polynôme est de degré 4.

T'as raison Doraki, c'est louche. J'imagine que si la méthode est bien faite, à partir d'un certains rang il n'y a qu'un seul minimum.

Salut tout le monde, Je bloque sur un problème de pénalisation en optimisation. Voici mon problème. Je considère les fonctions J_n définies sur \mathbb{R}^2 par: J_n(x;y) = 2x^2 + 3xy + 2y^2 + n(x+0.5)^2(y+0.5)^2 On sait que chaque J_n admet un minimum sur \mathbb{R}^2 . On l...

Je suis un peu embêté parce que moi c'est l’événement \{ \sup X_n \geq 1 \} qui m'intéresse. Du coup, je suis passé au complémentaire et je m'intéresse à l'événement \{ \sup X_n < 1 \} . Mais on a pas: \{ \sup X_n <1 \} = \bigcap \{ X_n < 1 \} Par contre, un truc comme ça doit être vrai: \{ \sup X_n...

Justement, tout mon problème est l'écriture sous forme d'une intersection dénombrable.
J'ai du mal à voir laquelle prendre.

Salut tout le monde, Comment montrer le résultat suivant ? Soit Y et (X_n) des varibales aléatoires telles que Y est indépendante de toutes les (X_n). Alors, Y est indépendante du sup X_n. Je peux me contenter d'un résultat un peu plus faible. Il faudrait que j'arrive à montrer que les évènements su...

Toujours personne ?

L'évènement par rapport auquel je conditionne est l'évènement: on connait les n premiers X_i et on a obtenu exactement a fois X_i = 1. Sinon, j'entends pas temps d'arrêt la définition classique des temps d'arrêts. J'ai juste oublié de préciser la filtration associée. C'est en fait la filatration nat...

Personne ?

Salut tout le monde, Je m'intéresse cette fois à la marche aléatoire simple sur Z. Est-ce que vous êtes d'accord avec ça ? \sup_{T \in \mathcal{T}} \mathbb{E}\big(S_{n+T} \quad / \quad \exists!\{i_1,\ldots,i_a\} \subset [1;n] \quad X_{i_1}=\ldots=X_{i_a} = 1\big) = 2a-n + \sup_{T \in \mathca...

Personne ?

Je viens de me rendre compte que je suis passé un peu vite sur l'application du théorème d'arrêt. T(k;m) n'est pas borné donc je suis allé chercher mon théorème d'arrêt pour des temps d'arrêt non borné. La condition pour que ça marche ici, ce serait: \forall n \in \mathbb{N}^* \quad \big(\frac{q...

Salut tout le monde, J'ai une petite question sur le conditionnement. Un résultat me paraît vrai mais je n'arrive pas à voir pourquoi. Je me donne X_1,...,X_n des variables aléatoires iid. Alors l'espérance conditionnelle par rapport à X_1,...,X_n est en fait l'espérance conditionnelle par rapport à...

Merci pour tes réponses.
Je trouve ça très joli comme méthode. ^^