42 résultats trouvés
Revenir à la recherche avancée
En faite ce que je ne comprends pas c'est pourquoi le déterminant de la matrice admet une infinité de solution s'il vaut 0 ?
- 03 Juin 2010, 13:11
- Forum: ✯✎ Supérieur
- Sujet: extremum fonction à 2 variables
- Réponses: 5
- Vues: 1357
extremum fonction à 2 variables
Bonjour, On me demande trouver les extremums d'une fonction à 2 variables x1 et x2 avec un coefficient "m" inclus dans la fonction. q(x1; x2) = (m² + 1)(x1² + x2²) + 4mx1x2. On me demande : etudier suivant les valeurs de m les maxima et minima (locaux ou absolus) eventuels de q et la nature de ces...
- 01 Juin 2010, 16:56
- Forum: ✯✎ Supérieur
- Sujet: extremum fonction à 2 variables
- Réponses: 5
- Vues: 1357
dérivée partielles fonctions
Bonjour, J'ai quelques difficultés quant à la méthode pour la 1ère question. :mur: Comment prouver qu'elles sont liées ? et comment les dériver ? Les quantitées u; v; x; y; q sont liées par les relations suivantes q = f(x; y) ; x = u + v ; y = u - v 1. Vérifier que q est fonction de u et v et calcul...
- 03 Avr 2010, 15:47
- Forum: ✯✎ Supérieur
- Sujet: dérivée partielles fonctions
- Réponses: 1
- Vues: 749
- 03 Avr 2010, 15:36
- Forum: ✯✎ Supérieur
- Sujet: Dérivées partielles
- Réponses: 4
- Vues: 1179
Dérivées partielles
Bonjour, Je dois répondre aux questions, et j'ai un petit doute sur la question 3 Les prix unitaires des biens X et Y sont notées p et q. Les quantitées demandées des biens sont fonctions des 2 prix. On suppose que x = f(p; q) = \frac{100}{p^2q} et y = g(p; q) = \frac{100}{pq^2} . 1. Calculer les dé...
- 31 Mar 2010, 20:45
- Forum: ✯✎ Supérieur
- Sujet: Dérivées partielles
- Réponses: 4
- Vues: 1179
Matrice quadratique
Bonjour, A partir d'une matrice M, on m'a demandé de calculer tout un tas de chose, valeurs propres, vecteurs propres, matrice diagonale, matrice inversible... Puis vient la question où l'on m'a demandé de calculer la forme quadratique = q(v) = X^t M X ça c'est fait puis on me demande de déduire des...
- 19 Jan 2010, 19:42
- Forum: ✯✎ Supérieur
- Sujet: Matrice quadratique
- Réponses: 2
- Vues: 794
miikou a écrit:jte crois ..
jdisais juste que pour esperer avoir convergance il faut que le module soit inferieur a 1
je viens de toute refaire et je te remercie de ton coup de main, pour l'instant tout est bon et tout roule :zen:
- 15 Jan 2010, 13:35
- Forum: ✯✎ Supérieur
- Sujet: Matrice diagonale et limites
- Réponses: 11
- Vues: 1342
les valeurs propres sont bonnes et leurs sommes sont égales à 1 tout comme la trace de ma matrice M.
Je pense avoir tout juste jusqu'ici, je viens de faire le calcul de M^n.
D^n également.
Je pense avoir tout juste jusqu'ici, je viens de faire le calcul de M^n.
D^n également.
- 15 Jan 2010, 13:16
- Forum: ✯✎ Supérieur
- Sujet: Matrice diagonale et limites
- Réponses: 11
- Vues: 1342
- 15 Jan 2010, 13:07
- Forum: ✯✎ Supérieur
- Sujet: Matrice diagonale et limites
- Réponses: 11
- Vues: 1342
La réponse est évidement oui !!! Sauf que, dans ce type d'exo., les erreurs de calculs sont... trés fréquentes !!! Vu la quantité de calculs nécéssaire au calcul des sous espaces propre (i.e. de la matrice P) puis au calcul de P^{-1}, quand on a le temps , je conseillerais fortement de vérifier que...
- 15 Jan 2010, 13:04
- Forum: ✯✎ Supérieur
- Sujet: Matrice diagonale et limites
- Réponses: 11
- Vues: 1342
je ne trouve pas la même chose :cry: Pourtant P est bon car c'est la matrice des vecteurs propres de M qui est donnée dans l'énoncé sauf un que j'ai calculé ! P-1 je l'ai calculé, je l'ai vérifié également sous excel et on s'accorde sur la même chose. P-1MP = D (là je trouve bien tous mes vecteurs p...
- 15 Jan 2010, 12:57
- Forum: ✯✎ Supérieur
- Sujet: Matrice diagonale et limites
- Réponses: 11
- Vues: 1342
Bonjour, Si la matrice D est diagonale, le calcul de D^n est... trés simple. Essaye par exemple avec une matrice 3x3 : \left(\matrix{a&0&0\cr0&b&0\cr0&0&c\right)\left(\matrix{a&0&0\cr0&b&0\cr0&0&c\right)=... \left(\matrix{a&0&a...
- 15 Jan 2010, 11:29
- Forum: ✯✎ Supérieur
- Sujet: Matrice diagonale et limites
- Réponses: 11
- Vues: 1342
Matrice diagonale et limites
Bonjour,
On me demande de calculer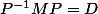 où D est une matrice diagonale.
où D est une matrice diagonale.
Ensuite on me demande de calculer et sa limite quand n tend vers l'infini et
et sa limite quand n tend vers l'infini et 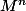
On me demande de calculer
Ensuite on me demande de calculer
- 15 Jan 2010, 11:15
- Forum: ✯✎ Supérieur
- Sujet: Matrice diagonale et limites
- Réponses: 11
- Vues: 1342
Mineurs diagonaux et valeurs propres
Bonjour,
On me demande de calculer les mineurs diagonaux d'une matrice après avoir trouvé les valeurs propres, on me demande si les mineurs sont en cohérence avec valeurs propres obtenues ?
Quel est le rapport ?
On me demande de calculer les mineurs diagonaux d'une matrice après avoir trouvé les valeurs propres, on me demande si les mineurs sont en cohérence avec valeurs propres obtenues ?
Quel est le rapport ?
- 13 Jan 2010, 13:15
- Forum: ✯✎ Supérieur
- Sujet: Mineurs diagonaux et valeurs propres
- Réponses: 1
- Vues: 1391
- 02 Déc 2009, 09:19
- Forum: ✯✎ Supérieur
- Sujet: dérivée fonction ln
- Réponses: 3
- Vues: 518
[quote="amath"]²
salut!
Le x en dernier peut-on le déplacer en premier;ce n'est pas mieux?sinon,je trouve:
pour 1 1.
salut!
Le x en dernier peut-on le déplacer en premier;ce n'est pas mieux?sinon,je trouve:
pour 1 1.
- 01 Déc 2009, 16:49
- Forum: ✯✎ Supérieur
- Sujet: dérivée fonction ln
- Réponses: 3
- Vues: 518
dérivée fonction ln
Bonjour,
je dois calculer la dérivée sur les deux intervalles.
J'ai trouvé ça :
ln x + ln |x - 1| - ln (x² - 2x + 1) + x
Df : ]0 , 1[ U ]1 ; +infini [
]0 , 1 [
-x² + x + 1
-----------
-x² + x
]1 , + infini[
x² - x -1
---------
x² - x
Pensez vous que c'est bon ?
je dois calculer la dérivée sur les deux intervalles.
J'ai trouvé ça :
ln x + ln |x - 1| - ln (x² - 2x + 1) + x
Df : ]0 , 1[ U ]1 ; +infini [
]0 , 1 [
-x² + x + 1
-----------
-x² + x
]1 , + infini[
x² - x -1
---------
x² - x
Pensez vous que c'est bon ?
- 01 Déc 2009, 11:57
- Forum: ✯✎ Supérieur
- Sujet: dérivée fonction ln
- Réponses: 3
- Vues: 518
Nightmare a écrit:Salut,
x²-2x+1=|x-1|². Donc l'expression de ta fonction se réduit en ln(x)+ln|x-1|-ln|x-1|²+x=ln(x)-ln|x-1|+x qui tend donc vers +oo en 1.
je trouve bien quelque chose qui ressemble à ça.
- 01 Déc 2009, 11:51
- Forum: ✯✎ Supérieur
- Sujet: Limites d'une fonction
- Réponses: 4
- Vues: 542
non désolé, en faite oui je voulais dire additionner le terme la série de terme n et la série de terme n +1.
- 01 Déc 2009, 11:50
- Forum: ✯✎ Supérieur
- Sujet: somme d'une série de terme
- Réponses: 4
- Vues: 854
somme d'une série de terme
Bonjour,
on me demande de calculer la somme de la série de terme :
[(-1)^n+1 (2n+1)] / n(n+1)
On calcule la somme en faisant la différence entre le terme "n+1" et "n" ?
on me demande de calculer la somme de la série de terme :
[(-1)^n+1 (2n+1)] / n(n+1)
On calcule la somme en faisant la différence entre le terme "n+1" et "n" ?
- 30 Nov 2009, 13:59
- Forum: ✯✎ Supérieur
- Sujet: somme d'une série de terme
- Réponses: 4
- Vues: 854
- 42 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
