Forum de Mathématiques: Maths-Forum

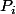
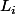
en fait je dois montrer que devient lorsqu'on utilise le procédé de Scmidt.

Donc je pense que la solution est une récurrence sur i, mais je n'arrive pas a la faire.
Et désolé Nuwanda, mais je ne comprend pas ce que tu as voulu m'expliquer.

désolé, j'ai oublier de préciser le produit scalaire: c'est:

avec

bonjour, on a: \forall k\in \left{1,..,n\right} , 3$ P_k=\prod_{j=k+1}^{n+1}(x_j-X) \hspace{5} et \hspace{5} P_{n+1}=1 On sait que la famille P_k est base de 2$ \R_n[X] . Montrer que la base orthormée déduite par la procédé de Schmidt est (L_1,L_2,...,L_{n+1}) avec : 3$ L_i=\prod_{j=...