Forum de Mathématiques: Maths-Forum

Quelle idée de faire un produit infini non dénombrable d'ensembles d'ailleurs ! Ça pourrait très bien être vide, même si aucun des ensembles ne l'est :zen: ! Je vais créer une pétition contre cette habitude absolument pas justifiée qu'ont les mathématiciens de choisir des choses parmi des produits i...

Je ne comprends pas ce que tu veux faire : tu n'arrives pas à montrer que x=0, ou alors tu l'as fait mais ça t'étonne ? Ça donne simplement que les points d'intersection ont pour abscisse le milieu de ce segment, ce qui est vrai (on le voit sur un dessin comme le dit Simon) donc il n'y a pas de prob...

Essaye de minorer le cardinal de

Oui ! (Plus précisément, "dérivable en 0")

De rien.
Pour borner les coefficients (toujours intéressant de voir plusieurs méthodes !), et bien on sait qu'ils s'écrivent comme des cos et des sin, donc c'est vite fait !

Oui ;) Et donc, que peut-on conclure pour la fonction ?

Les endomorphismes orthogonaux préservent la norme, on en déduit directement quelque chose sur leur norme à eux.

Non. Quelle est la limite de 1/x quand x tend vers 0, x>0 ? (Ou pour vraiment se mettre au milieu).

Tu peux aussi tracer la courbe de la fonction racine par exemple, et regarder la pente de la tangente. C'est sensé se correspondre

Pourquoi tu ne pourrais pas avoir deux valeurs différentes ? Ça voudrait dire que les courbes des fonctions puissances ont toutes la même tangente en 0 ! Or ce n'est pas le cas : regarde la courbe de x -> x^2, elle est bien "plate" en 0, sa tangente en 0 a bien une pente nulle ;). Donc non, c'est bo...

Écrire correctement et .

Tu es simplement ramenée à étudier la limite de en .
Selon les valeurs de tu obtiens quelque chose de fini ou non. Et cela correspond en effet à la pente de la tangente en .

C'est normal, au temps pour moi : mon explication était du grand n'importe quoi :dodo:

Je t'invite à fixer un dans et à considérer l'ensemble 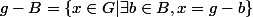, puis à étudier (combien d') les éléments qu'il partage avec A.

La première question que tu dois te poser c'est : "existe-t-il une façon simple d'écrire une fonction continue sur [0,1] comme une fonction constante, plus une fonction d'intégrale nulle" ;) ? Ensuite, il faut vérifier que cette écriture est unique. Ou alors que l'intersection de tes deux espaces es...

Ta piste est bonne. Poursuis en développant P(AnB) et consorts ;)

Re ;)

Ah oui ! J'ai complètement oublié la question de l'intégrabilité, quand on se ramène à des disques.

Au temps pour moi.

Du coup mes doutes sont levés et je vais pouvoir m'atteler à montrer que c'est bien un disque :p

Ah oui, pour les couronnes, j'ai dit n'importe quoi, puisque le centre n'est pas dedans... Mais si on prend un disque centré en z_0 et qu'on lui rajoute encore une couronne (donc de petit rayon plus grand que celui du disque), ça doit encore fonctionner non ? Il suffit d'écrire l'intégrale. Là où r ...

Personne pour poursuivre :) ?

Haha le monde est petit : j'étais justement en train de lire cet exo dans un bouquin. Ça a été posé à un oral ENS. En effet, est une bonne piste.

Bon, je vais arrêter là pour ce soir. Si quelqu'un arrive à trouver une fonction qui va bien, ce serait cool :D Par contre, deux choses que j'ai remarqué : -le résultat serait encore vrai pour les couronnes (cf mon édit en italique), et plus globalement, l'intérieur de toute union de cercles de cent...

Le résultat étant vrai, trouver un contre exemple risque d'être ardu ! Je parlais d'un contre exemple dans le cas où l'on prendrait un ouvert qui n'est pas un disque. Hmm, la mesure donc. Ok, merci. Edit : la mesure est invariante par rotation. Soit R la rotation de centre z_0 et d'angle \phi . Pou...