Forum de Mathématiques: Maths-Forum

professeur plutonium a écrit:tu n'as pas dit ce que c'était que , est-ce qu'il s'agit de la limite ( qui n'existe pas toujours ) de ?

Autant pour moi, j'édite le texte de l'énoncé.

Bonjour, Voici une question d'un problème sur laquelle je sèche. pourriez vous m'aider S.V.P.? On considère un nombre réel x et une suite réelle u . A tout réel strictement positif \epsilon , on associe la suite ( H _{m}( x, u, \epsilon))_{m\in\mathbb{N}} définie par : \forall m \in \mat...

OK, Mathelot, très bien!

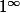
ne peut être égal à 1 puisque ce n'est pas un nombre.
est une écriture employée dans le langage des limites, mais ne peut intervenir dans une expression arithmétique.

Le seul sens qu'on peut lui attribuer est un type de forme indéterminée...

C'est bien une forme indéterminée, car on peut trouver différents cas où on aboutit à des résultats différents. Exemples: a) f(x)=exp(1/n) qui tend vers 1 en l'infini. g(x)=n qui tend vers l'infini en l'infini. f(x)^g(x) tend vers e en l'infini. b) f(x)=exp(2/n) qui tend vers 1 en l'infini. g(x)=n q...

Mathelot, j'ai essayé ta suggestion sans aboutir : \bigsum_{n=0}^{N} \frac{1}{(n+1)(2n+1) =-\bigsum_{n=0}^{N} \frac{1}{n+1} + 2\bigsum_{n=0}^{N} \frac{1}{2n+1} =-\bigsum_{n=0}^{N} \frac{1}{n+1} + 2(\bigsum_{n=0}^{2N} \frac{1}{n+1} - \bigsum_{n=1}^{N} \frac{1}{2n}) =-\bigsum_{...

Bonjour Mathelot,

Merci pour ta suggestion, mais je ne vois pas comment faire à partir de la série harmonique, où tous les termes sont positifs, pour arriver à la série de l'énoncé. Pourrais-tu donner d'autres indications?

Et bien voilà, tout s'arrange! Merci beaucoup pour cette précision importante!

Merci à tous! Je pense que vous avez tous raison : Mon erreur est d'avoir à tort supposé que cette convergence était uniforme pour passer à la limite. Mathmoica, ma méthode sûre rejoint la tienne. Le seul problème est que le rayon de convergence de ln(1+t) est ]-1;1[. Il faut donc au préalable prouv...

Bonjour! L'exercice qui me pose un problème est le suivant : Calculer \bigsum_{n=0}^{\infty} \frac{1}{(n+1)(2n+1)} en utilisant une série entière. J'ai déjà réussi à trouver le résultat (2ln2) par un autre moyen sûr. En revanche, par une série entière, je trouve seulement ln2, ce qui...

Bonjour et merci beaucoup, Yos. Je m'atelle immédiatement à la tâche....
OK, j'ai réussi. Merci encore pour ce tuyau!

Voici un problème en 7 questions. Les 4 premières sont très simples. Je bloque sur la 5ème... merci d'avance! Bonjour ! Va lire le règlement avant de poster sur le forum Le but de l'exercice est de donner toutes les fractions irréductibles de dénominateur inférieur ou égal à 25 qui sont strictement ...

Merci, je pense avoir trouvé la démarche à suivre....

POLITESSE ? Je suis bloqué sur l'exercice suivant : Soit la suite (Un) définie par : U0>0 Un+1=exp(-Un)*Un On demande de trouver un équivalent de Un lorsque n tend vers l'infini. On suggère de passer par la convergence au sens de Cesaro, c'est à dire que si une suite (Un) converge vers une limite l...