Forum de Mathématiques: Maths-Forum

Bonjour à tous,

je suis bloqué par une équation sur le Monier MPSI exercice 0.1.2

2*i*Z+4-i=Z-4i l'inconnue est Z, d'après la correction, il vient:

(2*i-2)*Z=-4*i+i

Je ne comprends pas d'oû vient le -2 dans la parenthèse

merci d'avance pour vos réponses Cordialement le fouineur

Merci spike0789 pour cette brillante démonstration,

Je vais reprendre le calcul depuis le début.

Avec mes remerciements Cordialement lefouineur

Bonjour spike0789 et merci pour ta réponse rapide, Voila ce que j'ai trouvé: (1/2)*(n(n+1)(2n+1))/6 + (1/2)*(n(n+1))/2 + [n(n+1)^2]/2 =[(1/6)*(n(n+1))/2 + (n(n+1))/2]*[(2n+1)+(n+1)] + (1/2)*(n(n+1))/2 =[(1/6)*(n(n+1))/2 + (n(n+1))/2]*[3n+2] + (1/2)*(n(n+1))/2 =n(n+1)/12 + [n(n+1)(3n+2)]/2 + (1/2)* (...

bonjour rockleader et merci pour ton aide,

Si je multiple par 2 le premier terme pas de problème,je tombe sur du 1/6, par contre si je multiplie le deuxième par 2, je tombe sur du 1/2....

Je ne vois pas comment m'en sortir car je n'en ai jamais fait.

Cordialement le fouineur

Bonjour à tous, Je suis bloqué par ce qu'il y a dans le titre (après un calcul de sommes) L'expression à mettre en facteurs est: \frac{1}{2}*\frac{n(n+1)(2n+1)}{6}+ \frac{1}{2}*\frac{n(n+1)}{2}+ (n+1)* (\frac{n}{2}+ \frac{n^{2}}{2}) Et l'on doit trouver: \frac...

Merci beaucoup capitaine nuggets et Carpate,

J'ai lu vos messages et cette fois, j'ai bien tout compris.

Merci pour le temps passé à me répondre... Cordialement le fouineur

Bonjour et merci Carpate pour ta réponse rapide,

Je n'ai jamais calculé de produit auparavant, peut-tu m'indiquer la marche à suivre pour arriver au résultat?

Je te te remercie d'avance pour ta réponse Cordialement le fouineur

Bonjour et merci ampholite pour ta réponse rapide,

Le produit à calculer était: Pn(1)=

et les termes intermédiaires s'annulant mutuellement, il ne reste que le premier et le dernier que j'ai écrit plus haut dans mon premier message....

Bonjour à tous,

Dans le calcul d'un produit fini,on obtient Pn=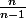 * =n+1

Je ne vois pas comment on obtient ça, pour moi Pn=
Si quelqu'un peut m'expliquer ça, je le remercie d'avance

Cordialement le fouineur

\int_x^{2x}\frac{t^2 +1}{(t^2*\sqrt{t^4+t^2+1})*(t^2+\sqrt{t^4+t^2+1}} dx = x\, \frac{t^2 +1}{(t^2*\sqrt{t^4+t^2+1})*(t^2+\sqrt{t^4+t^2+1}} C'est quoi le véritable énoncé ? Merci ev85 pour ta réponse rapide, Je n'ai pas pu mettre en entier l'énoncé car il est assez long, mai...

Bonjour à tous, Je bloque sur la transformation de l'expression suivante dans un corrigé d'exercice: \int_x^2x\frac{t^2 +1}{(t^2*\sqrt{t^4+t^2+1})*(t^2+\sqrt{t^4+t^2+1}dx Il faut lire "intégrale de x à 2x,et à la fin dx suit la fraction,toutes mes excuses mais je ne maîtrise pas le ...

merci mais par quelle démarche puis-je trouver ce résultat? :hein: Je l'ai trouvé à l'aide de Mathématica , mais il existe peut être des tables de transformées oû ton expression apparait....Il est inutile de vouloir démontrer l'expression que je t'ai donnée à la main: Tu risques de te retouver très...

Bonjour à tous, Je n'arrive pas à utiliser une fonction du programme analyse "Série(s) généralisée(s)"parce que je n'ai pas la bonne syntaxe de cette fonction.l'assistant suggère (Expression,variable,Ordre,[Point])mais "Point" écrit entre deux crochets appelle la fonction "Matrice" dont il n'est nul...

bonjour à tous, je me demande par où démarrer pour trouver la transformée de laplace de \frac {sh(x)}{x} j'ai jamais vraiment utilisé le sinus hyperbolique donc je suppose que je dois pouvoir le modifier pour trouver un équivalent plus utilisable? Merci d'avance ! Bonjour c'est tout simplem...

Sa Majesté a écrit:Les termes des 2 sommes s'annulent sauf un qui est

Merci Sa Majesté pour ton aide,l'algèbre n'est pas mon fort et c'est la première fois que je travaille avec des sommes.


Cordialement le fouineur

SaintAmand a écrit:Tu ne risques pas d'y arriver, il est faux. Que trouves-tu ?

En effet c'est le résultat que j'ai obtenu, la correction donne

Mille escuses pour l'erreur de saisie dans mon post précédent,et merci pour ton aide.

Cordialement le fouineur

Bonjour à tous, Je suis arrivé à un calcul incompris sur un problème de suites adjacentes: u(n-1)-v(n)= (\frac{1}{n+1} +\sum_{k=1}^{n+1}\frac{1}{k^2}) -(\frac{1}{n} +\sum_{k=1}^n\frac{1}{k^2}) le problème est que je ne comprends pas comment est obtenu le résultat qui ...

Merci BEN pour ta réponse rapide, Je te confirme que j'ai recopié exactement l'énoncé du problème,sans changer une virgule, et il n'apparait nulle part de fonction F dans l'énoncé. Pour t'en convaicre je te donne les coordonnées du livre et de l'exercice,tu pourras vérifier par toi même...... MATHEM...

Merci BEN de t'être penché sur mon problème, J'ai vérifié l'exactitude des termes de l'énoncé,et il apparait que les questions sont bien posées dans cet ordre là;j'ai étudié une autre fonction f(x) = \frac{sin x}{x} variant de 0 à l'infini aux questions 1o) ,2o) et 3o) du mème exercice mais ça n'a r...

Bonjour à tous, Je suis actuellement bloqué sur le problème suivant: (partie d'un énoncé dont j'ai résolu les trois premières questions) 4o)a)Etudier le signe de la fonction f(x)=tan(x)-x sur l'intervalle [0;Pi/2[ -en déduire le signe de f'(x) sur ]0;Pi/2[ b)Démontrer que pour tout entier naturel no...