Forum de Mathématiques: Maths-Forum

Zweig a écrit:Pour information, ce résultat porte le nom de théorème du papillon

Exact. Mais je n'ai découvert que c'était un théorème connu qu'après avoir mis le problème ici :lol5:

Bonne chasse aux angles, Lapras...

Bonsoir à tous ! :we:

Voilà un petit divertissement :

Tracez un cercle et une corde AB, de milieu M. Tracez ensuite les cordes PQ et RS passant par M. Les cordes PS et RQ coupent AB respectivement en U et V.

Montrez que M est le milieu du segment UV.

Bon anniversaire Alpha ! Tu peux maintenant te présenter à toutes les élections. Elle est pas belle la vie ? Nan, nan, nan...il faut avoir 23 ans pour se présenter à l'élection présidentielle, et 35 pour les élections sénatoriales....pour la présidence, on y est presque, pour le Sénat, y a encore d...

Alpha a écrit:Et 7+3=10, si je puis me permettre :id:

T'as trouvé ça tout seul ? :doh: Je suis épaté... :+++:

Le 7....bon, rien d'extraordinaire, j'imagine...mais le 7 a toujours eu une place particulière : sept merveilles du monde, sept planètes connues dans l'Antiquité, sept jours par semaine (que celui qui a dit "Blanche-neige et les sept nains" sorte :lol2:). Et d'un point de vue personnel, la...

Hello !
Sans utiliser de second degré, tu peux utiliser une solution géométrique : a²+b²=2 est l'équation du cercle de centre (0,0) et de rayon racine de 2, et a+b=1 est l'équation d'une droite : les deux nombres cherchés sont les coordonnées d'un point d'intersection entre la droite et le cercle.

Je serai dans la ville du pinard (Bordeaux), ce qui me permettra de boire pour oublier :lol2:

Merci ! Ca fait effectivement un bail que je n'étais pas venu ici (pour diverses raisons plus ou moins heureuses), je suis content de voir que tu te souviens de moi! :++: Pour le reste, je suis une vraie andouille...j'avais cartonné aux écrits, j'ai tout planté aux oraux, j'ai donc dû revoir mes amb...

Alpha a écrit:Maudits points en moins de 5/2... Il nous la font cher payer, quand même!

Je ne te le fais pas dire !

Ca n'a pas l'air d'inspirer les foules, lol.

Bonjour à tous !
Voilà l'énoncé du problème : calculer la somme des 1/n² en étudiant l'intégrale sur le pavé [0;1]² de 1/(1-xy). On montre facilement que l'intégrale est égale à la somme, mais comment calculer l'intégrale sans développer la fonction en série entière?

je crois que le sens est plutôt "souviens-toi qu'il faut mourir" (ie que la mort est inéluctable)

A-t-il vraiment refusé par modestie, ou au contraire pour attirer l'attention ?

On soumet à un mathématicien, à un physicien, à un informaticien et à un chimiste l'hypothèse suivante : "tout entier naturel impair supérieur ou égal à 3 est premier". Le mathématicien : "3 ça marche, 5 ça marche, 7 ça marche, 9 ça marche pas...elle est débile, votre hypothèse!"...

Sdec25 a écrit:Non les nombres complexes ne sont pas ordonnés comme les réels (on ne peut pas dire qu'un nombre est plus grand qu'un autre).

On peut les ordonner, mais ça ne sert à rien.

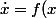nox a écrit:Alors toute solution de tend vers I

Une fonction qui tend vers un ensemble ????

nada-top a écrit:j'arrive pas à imaginer ce i , dans l'expression i² = -1 ,franchement il me parait un peu mystérieux

Ne te lance pas dans l'étude des quaternions, alors... :ptdr:

L'origine des complexes est la résolution des équations du 3ème degré ( Bombelli, je crois : au lieu de s'arrêter quand il tombait sur "racine de -1", il a poursuivi les calculs, et constaté que les résultats fonctionnaient La résolution des équations du troisième degré s'est faite en plu...

theorie a écrit: je réussis les éxo une fois sur deux... je m'en sort une fois sur deux.

Tu vois, tu parles déjà comme un probabiliste. :zen: