Forum de Mathématiques: Maths-Forum

Bonjour, je rencontre un problème concernant la détermination de géodésiques lumineux dans la métrique de Friedmann-Lemaitre-Walker-Robertson. Je me place dans un espace 2D, Je ne considère donc ici que les variables theta et r. Ces deux variables suivent la relation : [CENTER] \int_{r}^{r1}\,\frac{...

merci pour cette démo rapide, je me prenais la tete avec les angles alors qu'il y avait beaucoup plus simple.

bonsoir,

oui le tétraèdre est porté par les axes d'une base orthonormale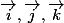 , quelle est alors cette solution analytique rapide permettant d'avoir ?

]bonsoir, je n'arrive pas à retrouver l'expression du vecteur S_t orthogonal à la surface ABC (cf image: http://forums.futura-sciences.com/attachments/mathematiques-superieur/74530d1239144688-probleme-demo-tetraedre-de-contraintes-tetra.png ), de longueur S_t et dirigé de l'intérieur du tétraèdre ve...

bonjour, je rencontre un problème lors de la démo suivante: \frac{d\,y^i}{d\alpha^}=\frac{d\,y^i}{d\beta} \,\,\frac{d\beta}{d\alpha} (eq°1) ce qui donne: \frac{d^2\,y^i}{d\alpha^2}=\frac{d^2\,y^i}{d\beta^2}\,\,\big(\frac{d\beta}{d\alpha}\big)^2+\frac{d\,y^i}{d\beta}\,\,\frac{d^2\beta}{d\,\al...

L'équation n°1 qui donne b_{ji}=g^{ij}=g^{ji} est vrai si et seulement si le tenseur fondamental de la métrique est symétrique, peut-il y'avoir des tenseurs fondamentaux de métrique non symétriques (que l'on peut rencontrer en relativité générale par exemple) ? , auquel cas j'ai toujours le même pro...

bonjour, j'ai un petit problème pour démontrer l'expression de la dérivée d'un déterminant, la seule démo que j'ai trouvé se trouve ici : http://www.sciences.ch/htmlfr/algebre/algebrelineaire01.php#derdet le soucis se situe dans l'équation (13.134), voici ce qui est marqué : b_{ji}=\frac{1}{det(...