Forum de Mathématiques: Maths-Forum

Bonjour,

Je dois trouver les valeurs de pour lesquelles l'équation différentielle suivante a une solution non triviale : et .

Des idées? :hein:

Merci!

Bonjour,

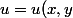Je dois démontrer que le système d'équations suivant définit implicitement les fonctions et .




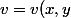Des idées?

Bonjour, Je dois résoudre le système d'équations différentielles suivant : \frac{dx}{dt} = -2x+3y \frac{dy}{dt}=x-y avec les conditions initiales x(0)=1 , y(0)=-1 . J'ai transformé la première équation (en considérant y comme une constante) : X(s)=-2\frac{1}{s^3}+3y\frac{1}{s...

J'obtiens, en dérivant par rapport à x : 4u^2+8xu\frac{\partial u}{\partial x}+y\frac{\partial v}{\partial x} 4yv\frac{\partial v}{\partial x}+u+x\frac{\partial u}{\partial x}=0 Puis, par rapport à y : 8xu\frac{\partial u}{\partial y}+v+y\frac{\partial v}{\partial y}=0 2v^2+4yv\frac{\partial v}{\par...

Bonjour,

Si les équations et définissent et près du point et , comment calculer et ? :hein:

Merci!

Bonjour, La surface x^7y^2+y^6z^7+z^9x^7+6xyz=9 a comme équation z=f(x,y) au voisinage du point (1,1,1) ( f(x,y) étant différentiable en ce point). Trouvez \frac{\partial f}{\partial x}(1,1) et \frac{\partial^2f}{\partial x^2}(1,1) . Je ne vois pas comment m'y...

Bonjour, Nous avons vu en classe que le Wronskian servait à vérifier si les solutions à une équation différentielle sont linéairement indépendantes. W(y_1,y_2,...,y_n)(x) \neq 0 alors les solutions y_1,y_2,...y_n sont linéairement indépendantes au point x. Le prof nous a aussi démont...

mathelot a écrit:non ?

Très juste!

Merci beaucoup pour votre aide!

x_1 = -2+(a-4)i x_2 = -2-(a-4)i y(x) = C_1y_1(x)+C_2y_2(x) y(x) = C_1e^{-2x}cos((a-4)x)+C_2e^{-2x}sin((a-4)x) Posons x=0, y=0 : 0= C_1cos(0)+C_2sin(0) C_1=0 Posons x=6, y=0 : 0 = C_2e^{-12}sin((a...

x_1 = -2+\sqrt{4-a} x_2 = -2-\sqrt{4-a} y(x) = C_1y_1(x)+C_2y_2(x) y(x) = C_1e^{(-2+\sqrt{4-a})x}+C_2e^{(-2-\sqrt{4-a})x} Posons x=0, y=0 : 0 = C_1+C_2 C_2 = -C_1 y(x) = C_1e^{(-2+\sqrt{4-a})x}-C_1e^{(-2-\sqrt{4-a})x} y(x&#...

Bonjour,

Je dois trouver les 3 plus petites valeurs de qui satisfont cette l'équation différentielle :


,

Quelqu'un peut me donner une piste?

Merci! :happy2:

Je ne vois pas comment passer de à ... Pourrais-tu me donner plus de détails?

Merci :happy2: !

Bonjour,

Je dois démontrer que l'équation différentielle a un facteur d'intégration qui est fonction de si et seulement si est fonction de z seulement.

Comment faire? :hein3:

\sum_{n=0}^{\infty}(n+2)(n+1)a_{n+2}t^n-\sum_{n=0}^{\infty}(n+2)(n+1)a_{n+2}t^{n+2} {-}\sum_{n=0}^{\infty}na_{n}t^{n+1}-\sum_{n=0}^{\infty}a_{n}t^{n+1}-\sum_{n=0}^{\infty}(-1)^nt^{2n}{\frac{1}{2} \choose n}=0 \sum_{n=0}^{\infty}\left( (n+2)(n+...

J'obtiens :



Je suis toujours pris avec ... Que faire ensuite?

Je parle de séries de puissances entières, pardon.

Dans ta deuxième réponse, tu dis qu'il faut développer et en séries de puissances entières, mais je ne vois pas comment. Pourrais-tu m'expliquer?

Bonjour, J'essaie de résoudre y^{\prime\prime}-sin(x)y=cos(x) avec les séries sachant que y(0)=-5 et y'(0)=3 . J'ai posé : y=\sum_{n=0}^{\infty} a_{n}x^n y^{\prime\prime}=\sum_{n=0}^{\infty} (n+2)(n+1)a_{n+2}x^n et j'ai remplacé sin(x) et c...

Merci grikor! Voici la démarche complète pour ceux qui tombent sur un problème similaire : 5y^4-11x^2y^2-30x^4-(6xy^3)\frac{dy}{dx}=0 Changement de variable : y = xz dy = zdx+xdz 5x^4z^4-11x^4z^2-30x^4-6x^4z^3\frac{zdx+xdz}{dx}=0 5x^4z^4-11x^4z^2-30x^4-6x^4z^4-6x^5z^3\frac{dz}{dx}=0 (-x^...

Après avoir fait la substitution, j'arrive à z^4+11z^2+30+6xz^3\frac{dz}{dx}=0 et donc \frac{\partial M}{\partial z}= 4z^3+22z \frac{\partial N}{\partial x}=6z^3 q(z)=\frac{\frac{\partial M}{\partial z}-\frac{\partial N}{\partial x}}{M}=\frac{22z-2z^3}{z^4+11z^2+30} Comme q est fonction de z...

Bonjour, J'essaie de trouver les solutions (forme generale) de l'equation differentielle suivante : 5y^4-11x^2y^2-30x^4+(-6xy^3)\frac{dy}{dx}=0 Nous avons vu en classe qu'il est possible de rendre exacte une equation differentielle de ce genre en la multipliant par un facteur d'integration u...