Forum de Mathématiques: Maths-Forum

Mes intégrales ne sont égales à l'espérance que pour t=\infty dans le cas général ou pour t suffisamment grand dans mes hypothèses. Sinon, ça n'est pas l'espérance, et comme l'inégalité doit être vérifiée pour tout t, on arrive à \mathbb{E}\[ W(\eta)\]\geq \mathbb{E}\[ W(\xi)\] pour ...

Euh non, je me reprends... Ma conjecture n'est bonne que pour

Du coup, il faut s'intéresser à l'image des variables aléatoires par des fonctions convexes décroissantes...

Bon je viens d'écrire le calcul pour un univers et ma conjecture est bonne!

En fait, c'est ce t qui est trompeur dans la définition avec les intégrale, parce q'il ne correspond pas au temps qui passe!

Bonjour, On définit la dominance stochastique entre deux variables aléatoires par: \xi \succeq \eta ssi: \forall t\geq 0 \int_0^t\mathbb{P}(\xi\geq x)dx\geq\int_0^t\mathbb{P}(\eta\geq x)dx Est ce que quelqu'un pourrait me dire comment je traduis ça en horizon fini, avec |\Omega|<\inf...

elle contient au moins deux cartes identiques?

Bonjour, Je bloque un peu sur ce problème, voici l'énoncé: On prend un jeu de 52 cartes qu'on répartit en 13 tas de 4 cartes. Montrer que quelle que soit cette répartition, on pourra toujours prendre une carte de chacun des tas et ainsi reconstituer la suite {as,2,3,4,5,6,7,8,9,10,valet,dame,roi}. J...

Je reviens sur le "il suffit de travailler comme avec des espaces vectoriels en parlant de rang plutôt que de dimension..." Ne montre-t-on pas alors que R*,S* = R,S...? Dans l'énoncé de l'exo, on doit montrer que S*,R* = R,S, où R \subset S sont des R0 modules... J'avoue là je suis complèt...

Alors qu'est ce que ce (S,R) veut dire???

ok. Quelle est ta définition de (S:R) ? Ben justement je ne suis pas certain et ce n'est pas dans mon cours... JE n'ai pas trouvé de définition formelle dans la littérature (par ailleurs pas très fournie dans ce domaine dans mon uniiversité)... Est-ce qu'on n'aurait pas: (S:R) = rang de S sur R, à ...

Bonsoir,

D'accord sur la définition des ordres... Sur votre débat, je suis encore au début de mes cours de Théorie des nombres, je ne saisis pas encore très bien les différences conceptuelles!

Comment dois-je donc utiliser ces indications pour prouver mon égalité?
Merci

Je suis d'accord... Donc l'exercice serait faux/mal posé?

C'est le dual...


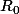étant maximal, je vois mal comment il pourrait être contenu dans R!!!

D'ailleurs, tous ces ordres sont des modules libres de rang n non?

Bonjour, Une petite question: Si F est une extension de degré n d'un corps de base F_0 avec un ordre maximal R_0 et que R\subset S sont des ordres de F, Comment puis-je démontrer (S:R)=(R^* : S^*) en tant que R_0 -modules?? En fait je déjà je ne suis pas très familier avec les ordres...

Bonjour, Un petit problème de combinatoire sur lequel je bloque: On prend n arbres de telle sorte que si on en prend deux au hasard, il existe un et un seul pont entre eux. Il y a des petits singes qui vivent dans ces arbres (exactement un par arbre), et qui veulent aller rendre visite à tous leurs ...

Non ma question c'est

Mais est-ce que cette intégrale de Riemann est égale à l'intégrale de Stieltjes que tu as écrite toi?

Bonjour,

Une petite question de probabilité:

Soit Bs(w) un mouvement brownien standard pour s positif ou nul.

Comment je peux démontrer que l'intégrale de Bs pour s variant entre 0 et 1 suit une loi normale et calculer sa variance/espérance?

Merci de votre aide

Bonsoir, Non, aucune condition, sinon évidemment qu'on "s'autorise" les bornes infinies... A et B sont absolument quelconques... J'ai réussi à démontrer l'une des égalités, inf sup >= sup inf, il suffit d'écrire que les inf/sup sont les plus petits/grands des minorants/majorants et ça sort tout seul...

Bonjour, Je suis bloqué par le problème suivant, On considère une fonction de AxB dans R: f(x,y). Il faut que je prouve ou que je contredise les inégalités: sup { inf { f(x,y) , x } , y } <= inf { sup { f(x,y) , y } , x } sup { inf { f(x,y) , x } , y } >= inf { sup { f(x,y) , y } , x } Je ne trouve ...

Je crois que j'ai trouvé: on suppose que de N-k+1 à N, l'enveloppe de Snell du gain est égale au gain lu-même: pour tout i de cet intervalle, U(i) = i*Y(1)*Y(2)*...*Y(i) où Y(t) est la VA qui vaut 1 si la réponse est correcte et zéro si elle est fausse. on suppose que de N-k à 1, l'enveloppe de Snel...

Bonjour, petite question sur un quiz: à chaque bonne réponse je gagne 1; j'ai alors le droit de choisir entre arrêter le jeu ou répondre à une nouvelle question. si je réponds faux, je perds tout et le jeu est fini. il y a au plus N questions. les questions sont deux à deux indépendantes, et on répo...