Quel est ton soucis ?
Qu'as tu fais ? Ou est ce que tu bloques ?
204 résultats trouvés
Revenir à la recherche avancée
- 02 Nov 2010, 15:12
- Forum: ✎ Collège et Primaire
- Sujet: Dm géometrie thalès et pythagore
- Réponses: 5
- Vues: 1348
Hum. Quitte à passer pour une cruche, autant le faire à fond :
Je ne suis pas sur d'avoir compris.
Et surtout, ça ne me parle pas tellement. Je ne vois pas comment faire.
Je ne suis pas sur d'avoir compris.
Et surtout, ça ne me parle pas tellement. Je ne vois pas comment faire.
- 30 Oct 2010, 19:04
- Forum: ✯✎ Supérieur
- Sujet: Probabilité.
- Réponses: 4
- Vues: 543
Pour la densité, je l'ai calculé et j'ai trouvé \frac{1}{2\Pi} Après, pour les différentes variables aléatoires, on doit calculer les fonctions de répartition en partant de P(X \leq x) = P (cos (U) \leq x) etc. Et c'est là que je bloque totalement. Car pour se débarrasser du ...
- 30 Oct 2010, 18:38
- Forum: ✯✎ Supérieur
- Sujet: Probabilité.
- Réponses: 4
- Vues: 543
Probabilité.
Bonjour, bonjour ! J'ai un léger soucis en proba et je me demandais si quelqu'un pourrais m'aider. Voici l'énoncé : Soit U une variable aléatoire de loi uniforme [-\Pi ; \Pi] . Donner la densité et la fonction de répartition de U. Pour chacune des variables aléatoires suivantes, donner l'ensemble de...
- 30 Oct 2010, 17:59
- Forum: ✯✎ Supérieur
- Sujet: Probabilité.
- Réponses: 4
- Vues: 543
D'où mon premier post qui disait qu'il suffisait de chercher la dérivée, d'étudier son signe, etc, chose qu'elle savait déjà. On rempli par les valeurs et les limites, et je ne vois pas quoi ajouter de plus =/. à Aurel2402 : Pas de soucis ;). Et pour répondre à ta question, je suis en L1 MASS (mathé...
- 02 Mai 2010, 16:58
- Forum: ✎✎ Lycée
- Sujet: Derivée et tableau de variations.
- Réponses: 17
- Vues: 1415
Déjà, je ne vois pas en quoi sa dérivée n'est pas bonne. Et puis, je trouve ça plus intéressant de la laisser chercher plutôt que de donner directement les réponses. Quant à comment construire un tableau de variation, je pense qu'elle a saisi la chose : Calculer la dérivée, trouver son signe et en d...
- 02 Mai 2010, 16:55
- Forum: ✎✎ Lycée
- Sujet: Derivée et tableau de variations.
- Réponses: 17
- Vues: 1415
- 02 Mai 2010, 16:45
- Forum: ✎✎ Lycée
- Sujet: Derivée et tableau de variations.
- Réponses: 17
- Vues: 1415
- 02 Mai 2010, 16:41
- Forum: ✎✎ Lycée
- Sujet: Derivée et tableau de variations.
- Réponses: 17
- Vues: 1415
Essai de mettre sous la forme x à la puissance quelque chose * (ax²+b)
Comme ça, tu auras : = 0) , et donc tu pourras chercher :
, et donc tu pourras chercher :
 et
et
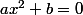
Comme ça, tu auras :
- 02 Mai 2010, 16:27
- Forum: ✎✎ Lycée
- Sujet: Derivée et tableau de variations.
- Réponses: 17
- Vues: 1415
Je ne vois pas ce qui te gène.
Pourquoi veux tu chercher x tel que f(x)=0 ?
Tu ne veux pas dire f'(x) plutôt ?
Et pour trouver f'(x)=0, met en facteur x de façon à te ramener à une forme que tu sais résoudre.
Pourquoi veux tu chercher x tel que f(x)=0 ?
Tu ne veux pas dire f'(x) plutôt ?
Et pour trouver f'(x)=0, met en facteur x de façon à te ramener à une forme que tu sais résoudre.
- 02 Mai 2010, 16:16
- Forum: ✎✎ Lycée
- Sujet: Derivée et tableau de variations.
- Réponses: 17
- Vues: 1415
- 02 Mai 2010, 16:06
- Forum: ✎✎ Lycée
- Sujet: Etude d'une fonction
- Réponses: 6
- Vues: 550
- 02 Mai 2010, 16:03
- Forum: ✎✎ Lycée
- Sujet: Derivée et tableau de variations.
- Réponses: 17
- Vues: 1415
- 02 Mai 2010, 15:53
- Forum: ✎✎ Lycée
- Sujet: Etude d'une fonction
- Réponses: 6
- Vues: 550
- 02 Mai 2010, 15:49
- Forum: ✎✎ Lycée
- Sujet: Derivée et tableau de variations.
- Réponses: 17
- Vues: 1415
Pour l'ensemble de définition, tu dois tout simplement éliminer les valeurs interdites donc ici : 
Quant à tes limites, vu que les cherchent en l'infini, il te suffit de mettre x en facteurs et de simplifier .
.
Quant à tes limites, vu que les cherchent en l'infini, il te suffit de mettre x en facteurs et de simplifier
- 02 Mai 2010, 15:39
- Forum: ✎✎ Lycée
- Sujet: Etude d'une fonction
- Réponses: 6
- Vues: 550
Merci pour tout, j'ai réussi à finir =D.
EDIT : Ah non zut, j'ai oublié la constante du dy/dx... (d'ailleurs, c'est pas plutôt dx/dy ??)
EDIT : Ah non zut, j'ai oublié la constante du dy/dx... (d'ailleurs, c'est pas plutôt dx/dy ??)
- 21 Avr 2010, 21:38
- Forum: ✯✎ Supérieur
- Sujet: Primitives
- Réponses: 10
- Vues: 757
- 21 Avr 2010, 21:26
- Forum: ✯✎ Supérieur
- Sujet: Primitives
- Réponses: 10
- Vues: 757
Ok. Avant de partir dans des calculs, petit point vérification : J'ai bidouiller mon numérateur ce qui m'a donné : \frac {x + 1}{sqrt {x^2 + 4x + 7}} = \frac {1}{2} \times \frac {2x + 4}{sqrt {x^2 + 4x + 7}} - \frac {2}{sqrt {x^2 + 4x + 7}} Donc j'ai mon \frac {u'}{ sqrt{u}} (d'ailleurs, je ne c...
- 21 Avr 2010, 21:21
- Forum: ✯✎ Supérieur
- Sujet: Primitives
- Réponses: 10
- Vues: 757
Merci beaucoup ! J'ai réussi en trouvant a = 1 et b = c = - 1 =). Hum. J'ai un autre soucis avec une autre primitive... Je ne sais juste pas comme l'attaquer. Je dois chercher la primitive de \frac {x + 1}{sqrt{x^2 + 4x + 7}} Donc je calcule mon discrimant pour pouvoir trouver une forme connu de rac...
- 21 Avr 2010, 20:58
- Forum: ✯✎ Supérieur
- Sujet: Primitives
- Réponses: 10
- Vues: 757
- 21 Avr 2010, 20:06
- Forum: ✯✎ Supérieur
- Sujet: Primitives
- Réponses: 10
- Vues: 757
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
